题目内容
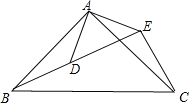
【题目】如图,已知A(-1,0),B(1,0),C为y轴正半轴上一点,点D为第三象限一动点,CD交AB于F,且∠ADB=2∠BAC,

(1)求证:∠ADB与∠ACB互补;
(2)求证:CD平分∠ADB;
(3)若在D点运动的过程中,始终有DC=DA+DB,在此过程中,∠BAC的度数是否变化?如果变化,请说明理由;如果不变,请求出∠BAC的度数.
【答案】(1)证明见解析;(2)证明见解析;(3)∠BAC=60°.
【解析】
(1)先判断△ABC是等腰三角形,然后在△ABC中利用三角形内角和定理以及∠ADB=2∠BAC即可得到结论;
(2)过点C作AM⊥DA于点M,作CN⊥BD于点N,运用“AAS”证明△CAM≌△CBN得CM=CN,根据“到角的两边距离相等的点在角的平分线上”得证;
(3)延长DB至点P,使BP=AD,连接CP,则可得CD=DP,证明△CAD≌△CBP,从而可得 △CDP是等边三角形,从而求∠BAC的度数.
(1)∵A(-1,0),B(1,0),
∴OA=OB=1,
∵CO⊥AB,
∴CA=CB,
∴∠ABC=∠BAC,
∵∠ABC+∠BAC+∠ACB=180°,∠ADB=2∠BAC,
∴∠ADB+∠ACB=180°,
即∠ADB与∠ACB互补;
(2)过点C作AM⊥DA于点M,作CN⊥BD于点N,则∠AMC=∠ANB=90°,

∵∠ADB+∠AMC+∠ANB+∠MCN=360°,
∴∠ADB+∠MCN=180°,
又∵∠ADB+∠ACB=180°,
∴∠MCN=∠ACB,
∴∠MCN-∠CAN=∠ACB-∠CAN,
即∠ACM=∠BCN,
又∵AB=AC,
∴△ACM≌△ABN (AAS),
∴AM=AN.
∴CD平分∠ADB(到角的两边距离相等的点在角的平分线上);
(3)∠BAC的度数不变化,
延长DB至点P,使BP=AD,连接CP,

∵CD=AD+BD,
∴CD=DP,
∵∠ADB+∠DBC+∠ACB+∠CAD=360°,∠ADB+∠ACB=180°,
∴∠CAD+∠CBD=180°,
∵∠CBD+∠CBP=180°,
∴∠CAD=∠CBP,
又∵CA=CB,
∴△CAD≌△CBP,
∴CD=CP,
∴CD=DP=CP,即△CDP是等边三角形,
∴∠CDP=60°,
∴∠ADB=2∠CDP=120°,
又∵∠ADB=2∠BAC,
∴∠BAC=60°.

 名校课堂系列答案
名校课堂系列答案