题目内容
已知关于x的一元二次方程(k-2)2x2+(2k+1)x+1=0有两个不相等的实数根,则k的取值范围是【 】
A.k> 且k≠2 且k≠2 | B.k≥ 且k≠2 且k≠2 | C.k > 且k≠2 且k≠2 | D.k≥ 且k≠2 且k≠2 |
C。
∵方程为一元二次方程,∴k-2≠0,即k≠2。
∵方程有两个不相等的实数根,∴△>0,
∴(2k+1)2-4(k-2)2>0,即(2k+1-2k+4)(2k+1+2k-4)>0,
∴5(4k-3)>0,k> 。
。
∴k的取值范围是k> 且k≠2。故选C。
且k≠2。故选C。
∵方程有两个不相等的实数根,∴△>0,
∴(2k+1)2-4(k-2)2>0,即(2k+1-2k+4)(2k+1+2k-4)>0,
∴5(4k-3)>0,k>
 。
。∴k的取值范围是k>
 且k≠2。故选C。
且k≠2。故选C。
练习册系列答案
相关题目
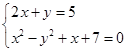 .
. 后经式子
后经式子 处理后得到一个结果.若这个结果大于0,则输出此结果;否则就将第一次得到的结果作为输入的
处理后得到一个结果.若这个结果大于0,则输出此结果;否则就将第一次得到的结果作为输入的 ,当初始端输入
,当初始端输入
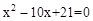 -的解,则第三边的长为【 】
-的解,则第三边的长为【 】 是关于
是关于 的一元二次方程,则
的一元二次方程,则 的取值范围是_______.
的取值范围是_______. 的值为( )
的值为( )