题目内容
若关于x的一元二次方程kx2+2(k+1)x+k﹣1=0有两个实数根,则k的取值范围是 ▲ .
k≥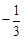 ,且k≠0
,且k≠0
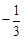 ,且k≠0
,且k≠0若一元二次方程有两不等实数根,则根的判别式△=b2﹣4ac≥0,建立关于k的不等式,求出k的取值范围.还要注意二次项系数不为0:
∵a=k,b=2(k+1),c=k﹣1,
∴△=[2(k+1)]2﹣4×k×(k﹣1)=8k+6≥0,解得:k≥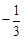 。
。
∵原方程是一元二次方程,∴k≠0。
∴k的取值范围是:k≥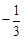 ,且k≠0
,且k≠0
∵a=k,b=2(k+1),c=k﹣1,
∴△=[2(k+1)]2﹣4×k×(k﹣1)=8k+6≥0,解得:k≥
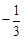 。
。∵原方程是一元二次方程,∴k≠0。
∴k的取值范围是:k≥
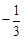 ,且k≠0
,且k≠0
练习册系列答案
相关题目
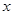 的一元二次方程
的一元二次方程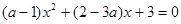 .
.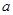 取不等于l的实数时,此方程总有两个实数根.
取不等于l的实数时,此方程总有两个实数根.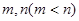 是此方程的两根,并且
是此方程的两根,并且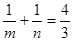 ,直线
,直线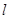 :
: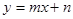 交
交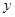 轴于点B,坐标原点O关于直线
轴于点B,坐标原点O关于直线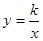 的图象上,求反比例函数
的图象上,求反比例函数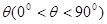 ,得到直线
,得到直线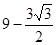 时,求角
时,求角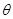 的值.
的值.

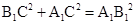 得方程 ,
得方程 , 且k≠2
且k≠2 且k≠2
且k≠2 配方后,原方程变形为( )
配方后,原方程变形为( )



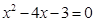 化成了
化成了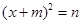 的形式,则m、n的值应为 ( )
的形式,则m、n的值应为 ( )  7
7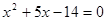 .
.