题目内容
若方程ax2=b（ab>0）的两个根分别是2m+5与4m+1，则
的值为（ ）
的值为（ ） | A．1 | B．2 | C．9 | D．4 |
C
解：∵ax2=b（ab＞0），
∴x2="b/a" ，
∴x=±b/a ，
即此方程的两根互为相反数，
∵方程ax2=b（ab＞0）的两个根分别是2m+5与4m+1，
∴2m+5+4m+1=0，
解得：m=-1，
∴2m+5=3，4m+1=-3，
∴b/a =9．
故选C．
∴x2="b/a" ，
∴x=±b/a ，
即此方程的两根互为相反数，
∵方程ax2=b（ab＞0）的两个根分别是2m+5与4m+1，
∴2m+5+4m+1=0，
解得：m=-1，
∴2m+5=3，4m+1=-3，
∴b/a =9．
故选C．
练习册系列答案
相关题目
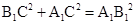得方程 ，
且k≠2
且k≠2
配方后，原方程变形为（ ）
； 
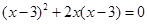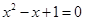的根的情况是