题目内容
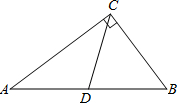
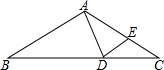
如图所示,AB=AC,∠A=120°,点E在AB边上,EF垂直平分AB,交BC于F,EG⊥BC,垂足为G,若GF=4,求CF的长.
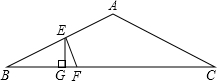

连接AF.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵EF⊥AB,EG⊥BF,
∴∠BEG+∠GEF=90°,又∠B+∠BEG=90°,
∴∠GEF=∠B=30°,
∵GF=4,
∴在Rt△GEF中,EF=2GF=8,
∴在Rt△BEF中,BF=2EF=16,
∵EF垂直平分AB,∴AF=BF=16,
∴∠BAF=∠B=30°,
∴∠FAC=120°-30°=90°,
又∵∠C=30°,
∴FC=2AF=32.
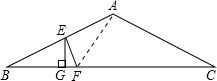
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵EF⊥AB,EG⊥BF,
∴∠BEG+∠GEF=90°,又∠B+∠BEG=90°,
∴∠GEF=∠B=30°,
∵GF=4,
∴在Rt△GEF中,EF=2GF=8,
∴在Rt△BEF中,BF=2EF=16,
∵EF垂直平分AB,∴AF=BF=16,
∴∠BAF=∠B=30°,
∴∠FAC=120°-30°=90°,
又∵∠C=30°,
∴FC=2AF=32.


练习册系列答案
相关题目