题目内容
如图,在平面直角坐标系xOy中,分别平行x、y轴的两直线a、b相交于点A(3,4),连接OA,若在直线a上存在点P,使△AOP是等腰三角形,那么所有满足条件的点P的坐标是( )
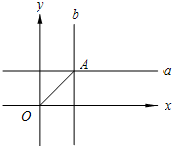
| A.(8,4) | ||
| B.(8,4)或(-3,4) | ||
| C.(8,4)或(-3,4)或(-2,4) | ||
D.(8,4)或(-3,4)或(-2,4)或(-
|
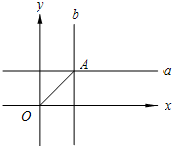
∵A(3,4),
∴OB=3,AB=4,
∴0A=
=5,
①若AP=OA,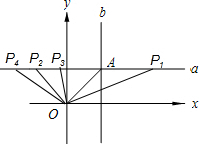 则点P的坐标为:(8,4)或(-2,4),
则点P的坐标为:(8,4)或(-2,4),
②若AP=OP,设点P的坐标为:(x,4),
则(x-3)2=x2+42,
解得:x=-
,
∴点P的坐标为(-
,4);
③若OA=OP,设P的坐标为(x,4),
则x2+42=52,
解得:x=±3,
∴点P的坐标为:(-3,4);
∴所有满足条件的点P的坐标是:(8,4)或(-2,4)或(-
,4)或(-3,4).
故选:D.
∴OB=3,AB=4,
∴0A=
| OB2+AB2 |
①若AP=OA,
 则点P的坐标为:(8,4)或(-2,4),
则点P的坐标为:(8,4)或(-2,4),②若AP=OP,设点P的坐标为:(x,4),
则(x-3)2=x2+42,
解得:x=-
| 7 |
| 6 |
∴点P的坐标为(-
| 7 |
| 6 |
③若OA=OP,设P的坐标为(x,4),
则x2+42=52,
解得:x=±3,
∴点P的坐标为:(-3,4);
∴所有满足条件的点P的坐标是:(8,4)或(-2,4)或(-
| 7 |
| 6 |
故选:D.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目