题目内容
【题目】解不等式组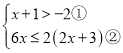
请结合题意填空，完成本题的解答.
（Ⅰ）解不等式①，得____________；
（Ⅱ）解不等式②，得____________；
（Ⅲ）把不等式①和②的解集在数轴上表示出来：
（Ⅳ）原不等式组的解集为_______．
【答案】（Ⅰ）
；（Ⅱ）
；（Ⅲ）图见解析；（Ⅳ）
．
【解析】
（Ⅰ）通过移项、合并同类项的步骤解不等式即可；
（Ⅱ）通过去括号、移项、合并同类项、系数化为1的步骤解不等式即可；
（Ⅲ）根据数轴的定义即可得；
（Ⅳ）由（Ⅲ）的结论即可得．
（Ⅰ）不等式
移项，得
合并同类项，得
故答案为：；
（Ⅱ）不等式
去括号，得
移项，得
合并同类项，得
系数化为1，得
故答案为：；
（Ⅲ）把不等式①和②的解集在数轴上表示如图所示：
（Ⅳ）由（Ⅲ）画出的数轴可知，原不等式组的解集为
故答案为：．
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
【题目】近一周，各个学校均在紧张有序地进行中考模拟考试，学生们通过模拟考试来调整自己的状态并了解自己的学业水平．某中学物理教研组想通过此次中考模拟的成绩来预估中考的各个分数段人数，在全年级随机抽取了男．女各40名学生的成绩（满分为80分，女生成绩中最低分为45分），并将数据进行整理分析，给出了下面部分信息：
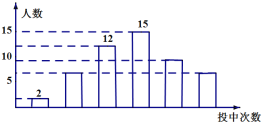
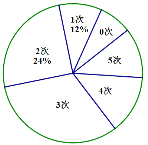
①男生成绩扇形统计图和女生成绩频数分布直方图如下：（数据分组为A组：x<50；B组：50≤x<60；C组：60≤x<70；D组：70≤x≤80）
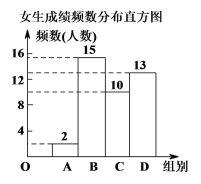
②男生C组中全部15名学生的成绩为：
63，69，64，62，68，69，65，69，65，66，67，61，67，66，69．
③两组数据的平均数．中位数．众数．满分率．极差（单位：分）如下表所示：
平均数 | 中位数 | 众数 | 满分率 | 极差 | |
男生 | 70 | b | c | 25% | 32 |
女生 | 70 | 68 | 78 | 15% | d |
（1）扇形统计图A组学生中所对应的圆心角α的度数为 ，中位数b= ，众数c= ，极差d= ．
（2）通过以上的数据分析，你认为 （填“男生”或“女生”）的物理成绩更好，并说明理由：
① ；② ．
（3）若成绩在70分（包含70分）以上为优秀，请你估计该校1200名学生中此次考试中优秀的人数．
【题目】水果基地为了选出适应市场需求的小西红柿秧苗，在条件基本相同的情况下，把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚，对市场最为关注的产量和产量的稳定性进行了抽样调查，过程如下:
收集数据从甲、乙两个大棚中分别随机收集了相同生产周期内25株秧苗生长出的小西红柿的个数：
甲：26，32，40，51，44，74，44，63，73，74，81，54，62，41，33，54，43，34，51，63，64，73，64，54，33
乙：27，35，46，55，48，36，47，68，82，48，57，66，75，27，36，57，57，66，58，61，71，38，47，46，71
整理数据按如下分组整理样本数据：
个数（x） 株数（株） 大棚 | 25≤x＜35 | 35≤x＜45 | 45≤x＜55 | 55≤x＜65 | 65≤x＜75 | 75≤x＜85 |
甲 | 5 |
| 5 |
| 4 | 1 |
乙 | 2 | 4 |
| 6 | 5 | 2 |
（说明：45个以下为产量不合格，45个及以上为产量合格，其中45≤x＜65个为产量良好，65≤x＜85个为产量优秀）
分析数据两组样本数据的平均数、众数和方差如下表所示：
大棚 | 平均数 | 众数 | 方差 |
甲 | 53 |
| 236.24 |
乙 | 53 | 57 | 215.04 |
得出结论
（1）补全上述表格；
（2）可以推断出 大棚的小西红柿秩苗品种更适应市场需求，理由为 （至少从两个不同的角度说明推断的合理性）；
（3）估计乙大棚的300株小西红柿秧苗中产量优秀的有多少株？