Question

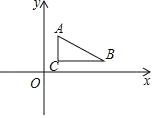
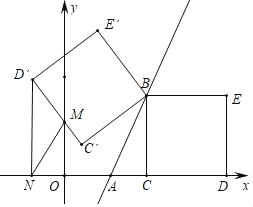
【题目】如图，两条射线BA//CD，PB和PC分别平分∠ABC和∠DCB，AD过点P，分别交AB，CD与点A，D．

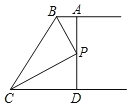
（1）求∠BPC的度数；

（2）若，求AB+CD的值；

（3）若为a，为b，为c，求证：a+b=c．

Answer 1

【答案】（1）90°；（2）4；（3）证明见解析

【解析】

（1）根据角平分线定义和平行线的性质，可得∠PBC+∠PCB的值，于是可求∠BPC的值；

（2）在△ABP，△PCD和△BCP中，利用特殊角在直角三角形中的边关系可求AB+CD的值．

（3）利用角平分线性质作垂直证明全等，通过割法获得面积关系．

（1）∵BA∥CD，∴∠ABC+∠BCD=180°．

∵PB和PC分别平分∠ABC和∠DCB，∴∠PBC∠ABC，∠PCB∠BCD，∴∠PBC+∠PCB（∠ABC+∠BCD）=90°，∴∠BPC=90°；

（2）若∠BCD=60°，BP=2，∴∠ABC=180°－60°=120°，∠PCD∠BCD=30°，∴∠ABP∠ABC=60°．

在Rt△ABP中，BP=2，AB=1．在Rt△BCP中，CP=2．在Rt△PCD中，PD，CD=3，∴AB+CD=4．

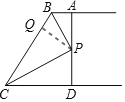
（3）如图，作PQ⊥BC．

∵∠ABP=∠QBP，∠BAP=∠BQP，BP=BP．

∴△ABP≌△BQP（AAS）．

同理△PQC≌△PCD（AAS），∴S△BCP=S△BPQ+S△PQC=S△ABP+S△PCD，∴a+b=c．