题目内容
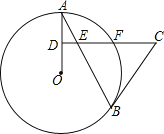
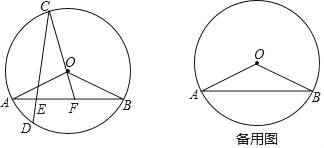
【题目】如图,在⊙O中,弦AB、CD相交于点E,![]() =
=![]() ,点D在
,点D在![]() 上,连接CO,并延长CO交线段AB于点F,连接OA、OB,且OA=
上,连接CO,并延长CO交线段AB于点F,连接OA、OB,且OA=![]() ,tan∠OBA=
,tan∠OBA=![]() .
.
(1)求证:∠OBA=∠OCD;
(2)当△AOF是直角三角形时,求EF的长;
(3)是否存在点F,使得S△CEF=4S△BOF,若存在,请求EF的长,若不存在,请说明理由.
【答案】(1)见解析;(2)EF=![]() 或
或![]() ;(3)存在
;(3)存在
【解析】
(1)先判断出∠ECB=∠EBC,再判断出∠OCB=∠OBC,即可得出结论;
(2)先求出EF,再分两种情况,利用锐角三角函数和相似三角形的性质即可得出结论;
(3)先利用面积关系得出![]() ,进而利用△OAF∽△EFC得出比例式,即可得出结论.
,进而利用△OAF∽△EFC得出比例式,即可得出结论.
解:(1)如图1,连接BC,
∵![]() ,
,
∴∠ECB=∠EBC,
∵OB=OC,
∴∠OCB=∠OBC,
∴∠OCD=∠ECF=∠ECB﹣∠OCB=∠EBC﹣∠OBC=∠OBA;
(2)∵OA=OB,
∴∠OAF=∠OBA,
∴∠OAF=∠ECF,
①当∠AFO=90°时,
∵OA=![]() ,tan∠OBA=
,tan∠OBA=![]() ,
,
∴OC=OA=![]() ,OF=1,AB=4,
,OF=1,AB=4,
∴EF=CFtan∠ECF=CFtan∠OBA=![]()
②当∠AOF=90°时,
∵OA=OB,
∴∠OAF=∠OBA,
∴tan∠OAF=tan∠OBA=![]() ,
,
∵OA=![]() ,
,
∴OF=OAtan∠OAF=![]() ,
,
∴AF=![]() ,
,
∵∠OAF=∠OBA=∠ECF,∠OFA=∠EFC,
∴△OFA∽△EFC,
∴![]() ,
,
∴EF=![]() OF=
OF=![]() ,
,
即:EF=![]() 或
或![]() ;
;
(3
∵∠ECB=∠EBC,
∴CE=EB,
∵OE=OE,OB=OC,
∴△OEC≌△OEB,
∴S△OEC=S△OEB,
∵S△CEF=4S△BOF,
∴S△CEO+S△EOF=4(S△BOE﹣S△EOF),
∴![]() ,
,
∴![]() ,
,
∴FO=![]() CO=
CO=![]() ,
,
∵△OFA∽△EFC,
∴![]() ,
,
∴BF=BE﹣EF=CE﹣EF=![]() EF,
EF,
∴AF=AB﹣BF=4﹣![]() EF,
EF,
∵△OAF∽△EFC,
∴![]() ,
,
∴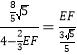 ,
,
∴EF=3﹣![]() .
.

【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?