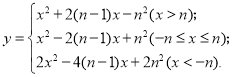题目内容
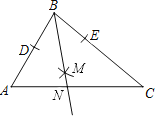
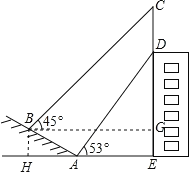
【题目】如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度![]() ,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,参考数据:tan53°≈
,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,参考数据:tan53°≈![]() ,cos53°≈0.60)
,cos53°≈0.60)

【答案】![]()
【解析】
过B作DE的垂线,设垂足为G,BH⊥AE.在△ADE解直角三角形求出DE的长,进而可求出EH即BG的长,在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长然后根据CD=CG+GE-DE即可求出宣传牌的高度.
解:过B作BG⊥DE于G,BH⊥AE,
Rt△ABH中,i=tan∠BAH=![]() =
=![]() ,
,
∴∠BAH=30°,
∴BH=![]() AB=5米;
AB=5米;
∴AH=5![]() 米,
米,![]()
∴BG=HE=AH+AE=(5![]() +21)米,
+21)米,
Rt△BGC中,∠CBG=45°,
∴CG=BG=(5![]() +21)米.
+21)米.
Rt△ADE中,∠DAE=53°,AE=21米,
∴DE=![]() AE=28米,
AE=28米,
∴CD=CG+GE﹣DE=26+5![]() ﹣28=(5
﹣28=(5![]() ﹣2)m.
﹣2)m.
答:宣传牌CD高为(![]() )米.
)米.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
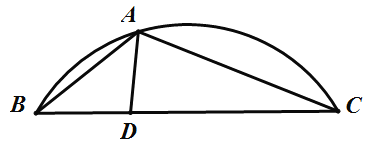
小夫子全能检测系列答案【题目】如图,A是![]() 上一动点,D是弦BC上一定点,连接AB,AC,AD.设线段AB的长是xcm,线段AC的长是
上一动点,D是弦BC上一定点,连接AB,AC,AD.设线段AB的长是xcm,线段AC的长是![]() cm,线段AD的长是
cm,线段AD的长是![]() cm.
cm.
小腾根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化的关系进行了探究.下面是小腾的探究过程,请补充完整:
随自变量x的变化的关系进行了探究.下面是小腾的探究过程,请补充完整:
(1)对于点A在![]() 上的不同位置,画图、测量,得到了
上的不同位置,画图、测量,得到了![]() ,
,![]() 的长度与x的几组值:
的长度与x的几组值:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | |
x/cm | 0.00 | 0.99 | 2.01 | 3.46 | 4.98 | 5.84 | 7.07 | 8.00 |
| 8.00 | 7.46 | 6.81 | 5.69 | 4.26 | 3.29 | 1.62 | 0.00 |
| 2.50 | 2.08 | 1.88 | 2.15 | 2.99 | 3.61 | 4.62 | m |
请直接写出上表中的m值是 ;
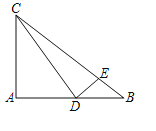
(2)在同一平面直角坐标系![]() 中,描出补全后表中各组数据所对应的点(x,
中,描出补全后表中各组数据所对应的点(x,![]() ),(x,
),(x,![]() ),并画出函数
),并画出函数![]() ,
,![]() 的图象;
的图象;
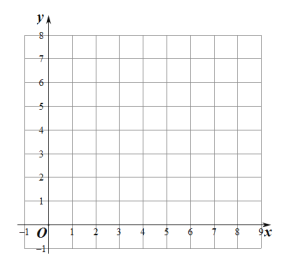
(3)结合函数图象,解决问题:当AC=AD时,AB的长度约为 cm;当AC=2AD时,AB的长度约为 cm.
【题目】为切实加强中小学生交通安全宣传教育,让学生真正知危险、会避险,郑州市某中学开展了“交通安全进校园”系列活动.为了解七、八年级学生对交通安全知识的掌握情况,对七、八年级学生进行了测试,现从两年级中各随机抽取20名学生的测试成绩(百分制)进行整理、描述和分析(成绩不低于90分为优秀).
测试成绩(百分制)如下:
七年级:52,78,82,86,77,83,92,87,72,81,93,98,81,69,87,86,80,81,82,94
八年级:87,77,90,79,93,83,88,84,82,94,86,88,57,68,89,59,81,90,88,95
分组整理,描述数据
分组 | 七年级 | 八年级 | ||
画“正”计数 | 频数 | 画“正”计数 | 频数 | |
| 一 | 1 |
| 2 |
| 一 | 1 | 一 | 1 |
|
|
| 2 | |
|
| 正正 | 10 | |
|
| 4 | 正 | 5 |
七、八年级抽取学生的测试成绩统计表
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 82 |
| 81 | 20% |
八年级 | 82.5 | 86.5 |
| 25% |
根据以上信息,回答下列问题:
(1)表中![]() __________,
__________,![]() __________,
__________,![]() __________,
__________,![]()
(2)若该校七年级270人和八年级280人参加了此次测试,估计参加此次测试成绩优秀的学生人数;
(3)根据以上数据,你认为该校七、八年级哪个年级学生掌握交通安全知识较好?并说明理由?