Question

【题目】直线与直线垂直相交于点，点在射线上运动（点不与点重合），点在射线上运动（点不与点重合）.

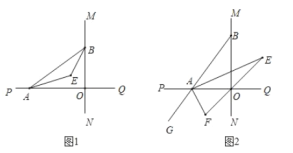
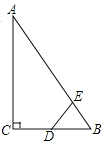
(1)如图1，已知、分别是和的角平分线，

①当时，求的度数；

②点在运动的过程中，的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出的大小；

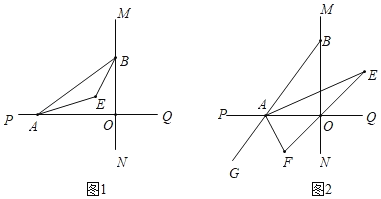
(2)如图2，延长至，已知、的角平分线与的角平分线所在的直线分别相交于、，在中，如果有一个角是另一个角的3倍，请直接写出的度数.

Answer 1

【答案】（1）∠AEB的大小不会发生变化，∠AEB的度数是135°；（2）60°或45°．理由见解析．

【解析】

（1）①根据三角形内角和定理、角分线定义即可求得∠AEB的度数；

②与①同理，只是把具体度数转化为角表示出来即可得结论；

（2）根据三角形内角和定理及一个外角等于与它不相邻的两个内角和，分四种情况讨论即可．

（1）如图1，①∵MN⊥PQ，∴∠AOB=90°．

∵∠ABO=60°，∴∠BAO=30°．

∵AE、BE分别是∠BAO和∠ABO的角平分线，∴∠ABE∠ABO=30°，∠BAE∠BAO=15°，∴∠AEB=180°﹣∠ABE﹣∠BAE=180°﹣30°－15°=135°．

答：∠AEB的度数是135°．

②∠AEB的大小不会发生变化．理由如下：

同①，得：∠AEB=180°﹣∠ABE﹣∠BAE=180°∠ABO∠BAO=180°（∠ABO+∠BAO）=180°90°=135°．

答：∠AEB的大小不会发生变化，∠AEB的度数是135°．

（2）∠ABO的度数为60°或45°．理由如下：

如图2．

∵∠BAO、∠OAG的角平分线与∠BOQ的角平分线所在的直线分别相交于E、F，∴∠OAE+∠OAF（∠BAO+∠GAO）=90°，即∠EAF=90°．

∵AE、OE是角平分线，∴∠BAE=∠EAO，∠BOE=∠EOQ，∴∠ABO +∠BAO=∠BOQ=90°=2∠EOQ=2（∠E+∠EAO），∴∠ABO +2∠EAO=2∠E+2∠EAO，∴∠E=∠ABO．

∵∠FAE=90°，∴∠F+∠E=90°，∴∠F=90°－∠E=90°－∠ABO．

分四种情况讨论：

①当∠FAE=3∠E时，∠E=90°÷3=30°，∠ABO =2∠E=60°；

②当∠FAE=3∠F时，∠F=90°÷3=30°，∴90°－∠ABO =30°，解得：∠ABO =120°＞90°，故舍去；

③当∠F=3∠E时，90°－∠ABO =3×∠ABO，解得：∠ABO =45°；

④当3∠F=∠E时，3×（90°－∠ABO）=∠ABO，解得：∠ABO =135°＞90°，故舍去．

综上所述：∠ABO的度数是60°或45°．

故答案为：60°或45°．