题目内容
【题目】如图,在平面直角坐标系xOy中,已知点A(1,2),B(3,2),连接AB.若对于平面内一点P,线段AB上都存在点Q,使得PQ≤2,则称点P是线段AB的“影子”.
(1)在点C(0,1),D(2,![]() ),E(4,5)中,线段AB的”影子”是 .
),E(4,5)中,线段AB的”影子”是 .
(2)若点M(m,n)在直线y=-x+2上,且不是线段AB的“影子”,求m的取值范围.
(3)若直线y=![]() x+b上存在线段AB的“影子”,求b的取值范围以及“影子”构成的区域面积.
x+b上存在线段AB的“影子”,求b的取值范围以及“影子”构成的区域面积.
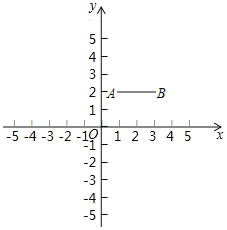
【答案】(1)C,D;(2)m<![]() 或m>2;;(3)4π+8.
或m>2;;(3)4π+8.
【解析】
(1)根据A、B的坐标得出AB∥x轴,根据点P到直线AB的距离≤2,求出当横坐标-1≤x≤3纵坐标2≤y≤4范围内时,点是线段AB的“临近点”,看点的纵坐标是否在y的范围内即可以及在A点的左边到A点的距离≤2,或在B点的右边到B点的距离≤2,点是线段AB的“临近点”;
(2)如图,设直线线y=-x+2交“影子”于点C,F,如图所示,延长BA交y轴于E,过C作CD⊥BA于BA的延长线于D,结合图形和一次函数图象上点的坐标特征来求m的范围;
(3)当直线y=![]() x+b与半圆A相切、与半圆B相切来求b的最值,从而得到b的取值范围.
x+b与半圆A相切、与半圆B相切来求b的最值,从而得到b的取值范围.
(1)C(0,1),D(2,![]() )是线段AB的“临近点”.理由是:
)是线段AB的“临近点”.理由是:
∵点P到直线AB的距离≤2,A、B的纵坐标都是2,
∴AB∥x轴,2-2=0,2+2=4,
∴当横坐标-1≤x≤3纵坐标2≤y≤4范围内时,该点是线段AB的“临近点”,
∵D(2,![]() ),
),
∴D(2,![]() )是线段AB的“临近点”;
)是线段AB的“临近点”;
∵C(0,1),A(1,2),
∴AC=1-0=1,
∴C(0,1)是线段AB的“临近点”.
故答案为:C和D;
(2)设直线线y=-x+2交“影子”于点C,F,如图所示,延长BA交y轴于E,过C作CD⊥BA于BA的延长线于D,
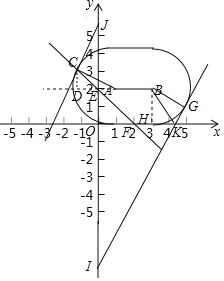
在Rt△ADC中,设D(x,2),则DE=-x,CD=-x,
∴DA=1-x,AC=2,
∴(-x)2+(1-x)2=4,
解得:x1=![]() ,x2=
,x2=![]() ,
,
∵直线y=-x+2与x轴的解得为F(2,0),
∴m<![]() 或m>2;
或m>2;
(3)设直线y=![]() x+b与半圆B相切于G,与x轴交于k,与y轴交于I,过B作BH⊥x轴于H,
x+b与半圆B相切于G,与x轴交于k,与y轴交于I,过B作BH⊥x轴于H,
则H(3,0),
在Rt△BHK中,BH=2,∠BKH=60°,
∴HK=![]() ,
,
在Rt△OKI中,OI=3![]() +2,则I(0,-3
+2,则I(0,-3![]() -2),
-2),
同理J(0,6-![]() ),
),
∴b的取值范围:-2-3![]() ≤b≤6-
≤b≤6-![]() ,
,
∵“影子”构成的区域为两个半圆和一个矩形,
∴影子”构成的区域面积=22π+4×2=4π+8.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案