题目内容
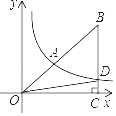
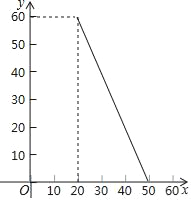
【题目】某商店经销一种小家电，每个小家电的成本为20元，市场调查发现，该种小家电每天的销售量y（个）与销售单价x（元）的函数图象如图．设这种小家电每天的销售利润为w元．
（1）求w与x之间的函数关系式；
（2）如果物价部门规定这种小家电的销售单价不高于32元，该商店销售这种小家电每天要获得400元的销售利润，销售单价应定为多少元？
【答案】（1）w=﹣2x2+140x﹣2000；（2）该商店销售这种小家电每天要获得400元的销售利润，销售单价应定为30元．
【解析】试题分析：（1）先求得销售量y（个）与销售单价x（元）的函数关系式，再根据“利润=销售量×（销售单价-成本）”即可得；
（2）将w=400代入（1）中的关系式，解方程后进行比较即可得.
试题解析：（1）设y=kx+b，
则
，
解得： 
，
则y=﹣2x+100（20≤x≤50），
所以w=（x﹣20）（﹣2x+100）=﹣2x2+140x﹣2000；
（2）根据题意，得：﹣2x2+140x﹣2000=400，
解得：x=30或x=40，
因为x≤32，
所以x=30，
答：该商店销售这种小家电每天要获得400元的销售利润，销售单价应定为30元．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
