题目内容
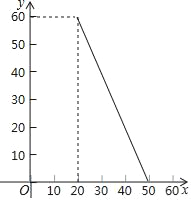
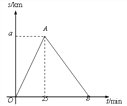
【题目】某市举行长跑比赛，运动员从甲地出发跑到乙地后，又沿原路线跑回起点甲地．如图是某运 动员离开甲地的路程 s（km）与跑步时间 t（min）之间的函数关系（OA、OB 均为线段）．已 知该运动员从甲地跑到乙地时的平均速度是 0.2 km/min，根据图像提供的信息，解答下列问 题：
（1）a＝ km；
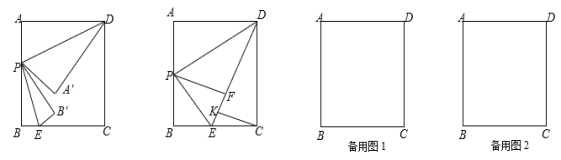
（2）组委会在距离起点甲地 3 km 处设立了一个拍摄点 P，该运动员从第一次过 P 点到第二
次过 P 点所用的时间为 24 min．
①求 AB 所在直线的函数表达式；
②该运动员跑完全程用时多少 min？
【答案】（1）5;(2) s＝
;(3) 60 min.
【解析】试题分析：（1）根据路程=速度×时间，即可求出a值；
（2）①根据点O、A的坐标，利用待定系数法即可求出线段OA的函数表达式，根据一次函数图象上点的坐标特征可求出第一次经过点P的时间，进而可得出第二次经过点P的时间，再根据点A的坐标及（39，3），利用待定系数法即可求出AB所在直线的函数表达式；
②根据一次函数图象上点的坐标特征，求出AB所在直线的函数表达式中当s=0时t的值，此题得解．
试题解析：解：（1）∵从甲地跑到乙地时的平均速度是0.2 km/min用时25分钟，∴a=0.2×25=5（千米）．故答案为：5．
（2）①设线段OA的函数表达式为s=mt+n，将O（0，0）、A（25，5）代入s=mt+n中，得： 
，解得：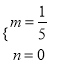 
，∴线段OA的函数表达式为s=
t（0≤t≤25），∴当s=
t=3时，t=15．∵该运动员从第一次过P点到第二次过P点所用的时间为24min，∴该运动员从起点到第二次经过P点所用的时间是15+24=39（min），∴直线AB经过点（25，5），（39，3）．设AB所在直线的函数表达式为s=kt+b，将（25，5）、（39，3）代入s=kt+b中，得： 
，解得：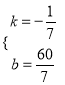 
，∴AB所在直线的函数表达式为s=﹣
t+
．
②该运动员跑完赛程用的时间即为直线AB与x轴交点的横坐标，∴当s=0时，﹣
t+
=0，解得：t=60，∴该运动员跑完赛程用时60分钟．
阅读快车系列答案
【题目】某农科所甲、乙试验田各有水稻3万个，为了考察水稻穗长的情况，于同一天在这两块试验田里分别随机抽取了
个稻穗进行测量，获得了它们的长度
（单位：cm），并对数据（穗长）进行了整理、描述和分析.下面给出了部分信息.
a.甲试验田穗长的频数分布统计表如下表所示（不完整）：
甲试验田穗长频数分布表
分组/ | 频数 | 频率 |
| 4 | 0.08 |
| 9 | 0.18 |
|
| |
| 11 | 0.22 |
|
| 0.20 |
| 2 | |
合计 | 50 | 1.00 |
b.乙试验田穗长的频数分布直方图如图所示：
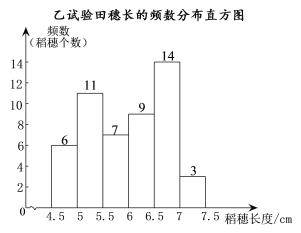
c.乙试验田穗长在
这一组的是：
6.3 6.4 6.3 6.3 6.2 6.2 6.1 6.2 6.4
d.甲、乙试验田穗长的平均数、中位数、众数、方差如下（表2）：
试验田 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 5.924 | 5.8 | 5.8 | 0.454 |
乙 | 5.924 |
| 6.5 | 0.608 |
根据以上信息，回答下列问题：
（1）表中
的值为 ，
的值为 ；
（2）表中
的值为 ；
（3）在此次考察中，稻穗生长（长度）较稳定的试验田是 ；
A．甲 B．乙 C．无法推断
（4）若穗长在
范围内的稻穗为“良好”，请估计甲试验田所有“良好”的水稻约为 万个．
