题目内容
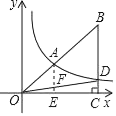
【题目】如图,双曲线y=![]() 经过Rt△BOC斜边上的点A,且满足
经过Rt△BOC斜边上的点A,且满足![]() ,与BC交于点D,S△BOD=21,求:
,与BC交于点D,S△BOD=21,求:
(1)S△BOC
(2)k的值.
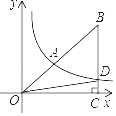
【答案】(1)S△BOC=25;(2)k=8
【解析】
(1)过点A作AE⊥OC于点E,交OD于点F,由平行线分线段成比例可得![]() =
=![]() =
=![]() =
=![]() ,利用面积比是相似比的平方得
,利用面积比是相似比的平方得![]() =
=![]() =
=![]() ,根据反比例函数图象性质得S△AOE=S△ODC,所以
,根据反比例函数图象性质得S△AOE=S△ODC,所以![]() =
=![]() =
=![]() ,进而△BOC的面积.(2) 设A(a,b),由(1)可得S△OCD=4 ,进而可得ab=8,从而求出k的值.
,进而△BOC的面积.(2) 设A(a,b),由(1)可得S△OCD=4 ,进而可得ab=8,从而求出k的值.
解:过点A作AE⊥OC于点E,交OD于点F,
∵AE∥BC, ![]() ,
,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∵ S△AOE=S△ODC,
∴![]() =
=![]() =
=![]() ,
,
∴S△BOC=25,
(2)设A(a,b),
∵点A在第一象限,
∴k=ab>0,
∵S△BOC=25,S△BOD=21,
∴S△OCD=4 即![]() ab=4,
ab=4,
∴ab=8,
∴k=8.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目