题目内容
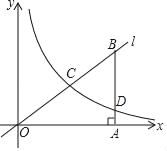
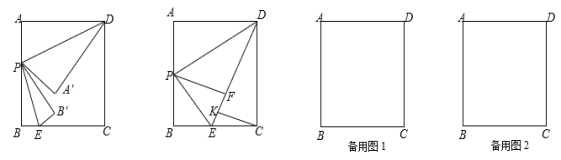
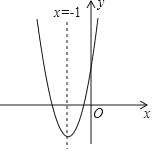
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c; ④4a﹣2b+c>0,其中正确有_____(填序号).
【答案】②③④
【解析】①∵抛物线与x轴有2个交点,∴△=b2﹣4ac>0,即b2>4ac,所以①错误;
②∵抛物线的对称轴在y轴的左侧,∴a、b同号,∴ab>0,
∵抛物线与y轴交点在x轴上方,∴c>0,∴abc>0,所以②正确;
③∵x=﹣1时,y<0,即a﹣b+c<0,
∵对称轴为直线x=﹣1,∴﹣ ![]() =﹣1,∴b=2a,∴a﹣2a+c<0,即a>c,
=﹣1,∴b=2a,∴a﹣2a+c<0,即a>c,
所以③正确;
④∵抛物线的对称轴为直线x=﹣1,∴x=﹣2和x=0时的函数值相等,即x=﹣2时,y>0,
∴4a﹣2b+c>0,所以④正确,
所以本题正确的有:②③④,
故答案为:②③④.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】某农科所甲、乙试验田各有水稻3万个,为了考察水稻穗长的情况,于同一天在这两块试验田里分别随机抽取了![]() 个稻穗进行测量,获得了它们的长度
个稻穗进行测量,获得了它们的长度![]() (单位:cm),并对数据(穗长)进行了整理、描述和分析.下面给出了部分信息.
(单位:cm),并对数据(穗长)进行了整理、描述和分析.下面给出了部分信息.
a.甲试验田穗长的频数分布统计表如下表所示(不完整):
甲试验田穗长频数分布表
分组/ | 频数 | 频率 |
| 4 | 0.08 |
| 9 | 0.18 |
|
| |
| 11 | 0.22 |
|
| 0.20 |
| 2 | |
合计 | 50 | 1.00 |
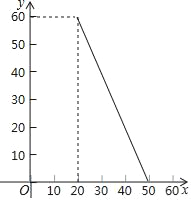
b.乙试验田穗长的频数分布直方图如图所示:
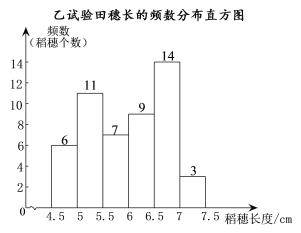
c.乙试验田穗长在![]() 这一组的是:
这一组的是:
6.3 6.4 6.3 6.3 6.2 6.2 6.1 6.2 6.4
d.甲、乙试验田穗长的平均数、中位数、众数、方差如下(表2):
试验田 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 5.924 | 5.8 | 5.8 | 0.454 |
乙 | 5.924 |
| 6.5 | 0.608 |
根据以上信息,回答下列问题:
(1)表中![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)表中![]() 的值为 ;
的值为 ;
(3)在此次考察中,稻穗生长(长度)较稳定的试验田是 ;
A.甲 B.乙 C.无法推断
(4)若穗长在![]() 范围内的稻穗为“良好”,请估计甲试验田所有“良好”的水稻约为 万个.
范围内的稻穗为“良好”,请估计甲试验田所有“良好”的水稻约为 万个.