题目内容
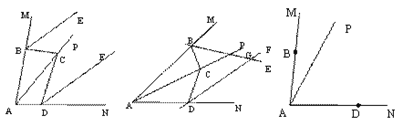
【题目】如图，点B、E分别在直线AC和DF上，若∠AGB=∠EHF，∠C=∠D，可以证明∠A=∠F．请完成下面证明过程中的各项“填空”．
证明：∵∠AGB=∠EHF（理由： ）
∠AGB= （对顶角相等）
∴∠EHF=∠DGF，∴DB∥EC（理由： ）
∴ =∠DBA（两直线平行，同位角相等）
又∵∠C=∠D，∴∠DBA=∠D，
∴DF∥ （内错角相等，两直线平行）
∴∠A=∠F（理由： ）．
【答案】已知；∠DGF；同位角相等，两直线平行；∠C； AC；∠A=∠F．
【解析】
分析: 根据对顶角相等推知同位角∠EHF=∠DGF，从而证得两直线DB∥EC；然后由平行线的性质知内错角∠DBA=∠D，即可根据平行线的判定定理推知两直线DF∥AC；最后由平行线的性质（两直线平行，内错角相等）证得∠A=∠F.
详解: ∵∠AGB=∠EHF（已知），∠AGB=∠DGF（对顶角相等），
∴∠EHF=∠DGF
∴DB∥EC（同位角相等，两直线平行），
∴∠C=∠DBA（两直线平行，同位角相等），
又∵∠C=∠D（已知），
∴∠DBA=∠D（等量代换），
∴DF∥AC（内错角相等，两直线平行），
∴∠A=∠F（两直线平行，内错角相等），
故答案是：已知；∠DGF；同位角相等，两直线平行；C；AC；两直线平行，内错角相等.
【题目】李老师为了了解学生暑期在家的阅读情况，随机调查了20名学生某一天的阅读小时数，具体情况统计如下：
阅读时间 （小时） | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数（名） | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是（ ）
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34
【题目】某体育老师对自己任教的55名男生进行一百米摸底测试，若规定男生成绩为16秒合格，下表是随机抽取的10名男生分A、B两组测试的成绩与合格标准的差值（比合格标准多的秒数为正，少的秒数为负）。
A 组 | -1.5 | +1.5 | -1 | -2 | -2 |
B组 | +1 | +3 | -3 | +2 | -3 |
（1）请你估算从55名男生中合格的人数大约是多少？
（2）通过相关的计算，说明哪个组的成绩比较均匀；
（3）至少举出三条理由说明A组成绩好于B组成绩，或找出一条理由来说明B组好于A组。
