Question

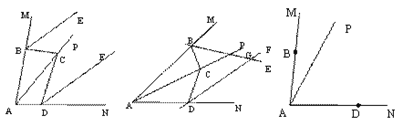
【题目】已知，点B、D分别在∠MAN的两边AM、AN上，点C是射线AP上的一点，连接BC、DC，∠MAN=α，∠BCD=β，(0°＜α＜180°，0°＜β＜180°)；BE平分∠MBC，DF平分∠NDC.

(1)如图1，若α=β=80°，

①求∠MBC+∠NDC的度数；

②判断BE、DF的位置关系，并说明理由.

(2)如图2，当点C在射线AP上运动时，若直线BE、DF相交于点G，请用含有α、β的代数式表示∠BGD.(直接写结果)

Answer 1

【答案】(1) ① 160°，② 平行；(2)①α- β，②β-α，③180°-α- β.

【解析】分析: (1) ①利用三角形外角即可求出; ②在①的基础上,再利用角平分线的性质即可求出;

(2)分情况,四边形BCDG是凸四边形,凹四边形来讨论.

详解: (1) ①α=β=80°,

∵∠MBC是△ABC的外角,

∴∠MBC=∠BAC+∠BCA,

同理, ∠NDC=∠DAC+∠ACD,

∴∠MBC+∠NDC=∠BAC+∠BCA+∠DAC+∠ACD

=∠MAN+∠BCD

=α+β

=160°

②BE∥DF

∵BE平分∠MBC, DF平分∠NDC,

∴∠EBC=∠MBC, ∠CDF=∠NDC,

∴∠EBC+∠CDF=(∠MBC+∠NDC)= ×160°=80°,

在△BCD中,

∵∠BCD=80°

∴∠CBD+∠CDB=100°

∴∠EBC+∠CBD+∠CDB=180°,

即∠EBD+∠FDB=180°,

∴BE∥DF(同旁内角互补,两直线平行)

(2)①α- β，②β-α，③180°-α- β.