题目内容
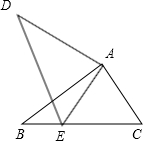
如图，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形，将四边形ACBD沿直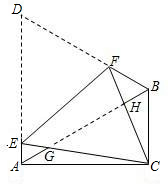
线EF折叠，使D与C重合，CE与CF分别交AB于点G、H．
（1）求证：△AEG∽△CHG；
（2）若BC=1，求cos∠CHG的值．
线EF折叠，使D与C重合，CE与CF分别交AB于点G、H．（1）求证：△AEG∽△CHG；
（2）若BC=1，求cos∠CHG的值．
（1）证明：∵△ABD是等边三角形，
∴∠EAG=∠D=60°；
根据折叠的性质知：DE=CE，∠D=∠GCH=∠EAG=60°，
又∵∠EGA=∠HGC，
∴△AEG∽△CHG．
（2）△ABC中，∠BAC=30°，BC=1，则AC=
，AB=2；
故AD=AB=2；
设DE=EC=x，则AE=2-x；
在Rt△AEC中，由勾股定理，得：
（2-x）2+3=x2，解得x=
；
∴AE=
，EC=
，
∴cos∠AEC=
=
；
由（1）的相似三角形知：∠AEG=∠CHG，
故cos∠CHG=cos∠AEC=
．
∴∠EAG=∠D=60°；
根据折叠的性质知：DE=CE，∠D=∠GCH=∠EAG=60°，
又∵∠EGA=∠HGC，
∴△AEG∽△CHG．
（2）△ABC中，∠BAC=30°，BC=1，则AC=
| 3 |
故AD=AB=2；
设DE=EC=x，则AE=2-x；
在Rt△AEC中，由勾股定理，得：
（2-x）2+3=x2，解得x=
| 7 |
| 4 |
∴AE=
| 1 |
| 4 |
| 7 |
| 4 |
∴cos∠AEC=
| AE |
| EC |
| 1 |
| 7 |
由（1）的相似三角形知：∠AEG=∠CHG，
故cos∠CHG=cos∠AEC=
| 1 |
| 7 |
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
