题目内容
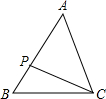
如图,在Rt△ABC中,∠B=90°,AB=BE=EF=FC.求证:△AEF∽△CEA.
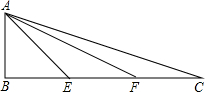

证明:设AB=BE=EF=FC=a,
∵∠B=90°,
∴在直角三角形ABE中,由勾股定理得AE=
a.
∵
=
=
,
=
=
,
∴
=
且∠AEF=∠CEA.
∴△AEF∽△CEA.
∵∠B=90°,
∴在直角三角形ABE中,由勾股定理得AE=
| 2 |
∵
| AE |
| EF |
| ||
| a |
| 2 |
| EC |
| AE |
| 2a | ||
|
| 2 |
∴
| AE |
| EF |
| EC |
| AE |
∴△AEF∽△CEA.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目

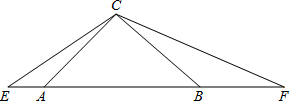
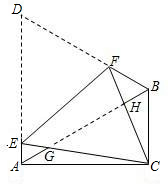 线EF折叠,使D与C重合,CE与CF分别交AB于点G、H.
线EF折叠,使D与C重合,CE与CF分别交AB于点G、H.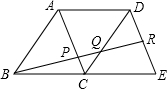 ,Q.
,Q.