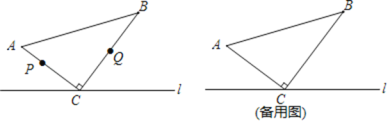题目内容
【题目】等边△ABC 的边长为 4,AD 是 BC 边上的中线,F 是边 AD 上的动点,E 是边 AC 上的点, 当 AE=2,且 EF+CF 取得最小值时.
(Ⅰ)能否求出∠ECF 的度数?_____(用“能”或“否”填空);
(Ⅱ)如果能,请你在图中作出点 F(保留作图痕迹,不写证明).并直接写出∠ECF 的度 数;如果不能,请说明理由.
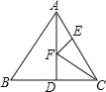
【答案】(Ⅰ)能;(Ⅱ)30°.
【解析】
(Ⅰ)过E作EM∥BC,交AD于N,连接CM交AD于F,连接EF,推出M为AB中点,求出E和M关于AD对称,根据等边三角形性质求出∠ACM,即可.
(Ⅱ)由(Ⅰ)的分析可得结论.
(Ⅰ)能;
(Ⅱ)过E作EM∥BC,交AD于N,
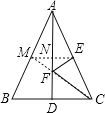
∵AC=4,AE=2,
∴EC=2=AE,
∴AM=BM=2,
∴AM=AE,
∵AD是BC边上的中线,△ABC是等边三角形,
∴AD⊥BC,
∵EM∥BC,
∴AD⊥EM,
∵AM=AE,
∴E和M关于AD对称,
连接CM交AD于F,连接EF,
则此时,EF+CF的值最小,
∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC,
∵AM=BM,
∴∠ECF=![]() ∠ACB=30°,
∠ACB=30°,
故答案为30°.

 走进文言文系列答案
走进文言文系列答案【题目】注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路,填写表格,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填写表格, 只需按照解答题的一般要求,进行解答即可.
某校八年级学生由距博物馆 10km 的学校出发前往参观,一部分同学骑自行车先走,过了20min 后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度 的 2 倍,求骑车同学的速度.
设骑车同学的速度为 xkm / h
(Ⅰ)根据题意,利用速度、时间、路程之间的关系,用含有 x 的式子填写下表:
速度(千米 / 时) | 所用时间(时 ) | 所走的路程(千米) | |
骑自行车 | x | 10 | |
乘汽车 | 10 |
(Ⅱ)列出方程,并求出问题的解.