��Ŀ����
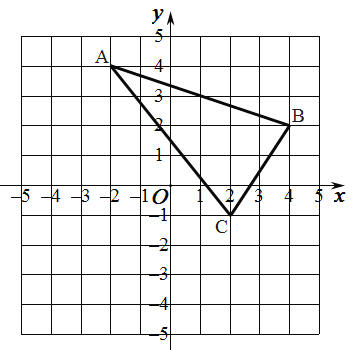
����Ŀ����������x�ύ��A��B����(��B�ڵ�A���Ҳ�)����A��B���������ֱ�Ϊ(-2��0)��(8��0)����y�ύ�ڵ�C(0��-4)������BC����BCΪһ������OΪ�Գ�����������BDEC����P��x���ϵ�һ�����������P������Ϊ(m��0)������P��x��Ĵ���L���������ڵ�Q����BD�ڵ�M.
(1)�������ߵĽ���ʽ��
(2)����P���߶�OB���˶�ʱ����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı���?
(3)λ�ڵ��������ڵ����������Ƿ���ڵ�N��ʹ�á�BCN��������?�����������N�������������BCN��������ֵ��������������˵������.

���𰸡�(1) �����߽���ʽΪy=![]() x2-
x2-![]() x-4��(2) ��m=4ʱ���ı���CQMD��ƽ���ı����� (3) S��BCN= 8.
x-4��(2) ��m=4ʱ���ı���CQMD��ƽ���ı����� (3) S��BCN= 8.
��������
��1���ô���ϵ����ֱ����������߽���ʽ��
��2�������εĶԳ��Կ�֪����D�����꣬���ݴ���ϵ��������ֱ��BD�Ľ���ʽ������ƽ���ı��ε����ʿɵù���m�ķ��̣����m��ֵ���ٸ���ƽ���ı��ε��ж��ɵ��ı���CQMD����״��
��3�����жϳ���N��ƽ����BC����������ֻ��һ������ʱ��λ�ã�ȷ������N�����꣬������Ͳ����������BCN�������
(1)�������ߵĽ���ʽΪy=ax2+bx+c��
��������ã�

�������߽���ʽΪy=![]() x2-
x2-![]() x-4.
x-4.
(2)��C(0��-4)��
�������εĶԳ��Կ�֪����D������Ϊ(0��4).
��ֱ��BD�Ľ���ʽΪy=kx+b'����![]() ���k=-
���k=-![]() ��b'=4.
��b'=4.
��ֱ��BD�Ľ���ʽΪy=-![]() x+4.
x+4.
��l��x�ᣬ
����M������Ϊ![]() ����Q������Ϊ
����Q������Ϊ![]() .
.
��ͼ����MQ=DCʱ���ı���CQMD��ƽ���ı��Σ�
��![]() =4-(-4).�����m2-4m=0�����m1=0(����������ȥ)��m2=4.
=4-(-4).�����m2-4m=0�����m1=0(����������ȥ)��m2=4.
����m=4ʱ���ı���CQMD��ƽ���ı���.
(3)���ڣ�����:
������Nƽ����ֱ��BC��ֱ����������ֻ��һ������ʱ����BCN��������.
��B(8��0)��C(0��-4)��
��BC=4![]() .ֱ��BC����ʽΪy=
.ֱ��BC����ʽΪy=![]() x-4�������Nƽ����ֱ��BC��ֱ��L������Ϊy=
x-4�������Nƽ����ֱ��BC��ֱ��L������Ϊy=![]() x+n����
x+n����
�������߽���ʽΪy=![]() x2-
x2-![]() x-4���������٢��ã�x2-8x-4(n+4)=0����
x-4���������٢��ã�x2-8x-4(n+4)=0����
����=64+16(n+4)=0��
��n=-8��
��ֱ��L����ʽΪy=![]() x-8����n=-8�������еã�x2-8x+16=0
x-8����n=-8�������еã�x2-8x+16=0
��x=4��
��y=-6��
��N(4��-6)��
��ͼ������N��NG��AB��

��S��BCN=S�ı���OCNG+S��MNG-S��OBC=![]() (4+6)��4+
(4+6)��4+![]() (8-4)��6-
(8-4)��6-![]() ��8��6=8.
��8��6=8.

 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�