题目内容
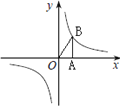
【题目】如图，直线l1过点A（8，0）、B（0，﹣5），直线l2过点C（0，﹣1），l1、l2相交于点D，且△DCB的面积等于8．
（1）求点D的坐标；
（2）点D的坐标是哪个二元一次方程组的解．
【答案】(1) D（4，﹣
）;(2) 
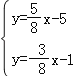
【解析】试题分析：（1）利用待定系数法求得直线l1的解析式，再求得点B、的坐标，根据三角形的面积公式即可求得点D的坐标；（2）求得直线l2的解析式，因l1、l2相交于点D，即可判定点D的坐标是哪个二元一次方程组的解．
试题解析：
（1）设直线l1的解析式为y=kx+b，
根据题意得：
，
解得：
，
∴直线l1的解析式为y=
x﹣5，
当x=0时，y=﹣5，
∴B（0，﹣5），
∴OB=5，
∵点C（0，﹣1），
∴OC=1，
∴BC=5﹣1=4，
设D（x，y），则△DCB的面积=
×4×|x|=8，
解得：x=±4（负值舍去），
∴x=4，代入y=x﹣5得：y=﹣
，
∴D（4，﹣）；
（2）设直线l2的解析式为y=ax+c，
根据题意得：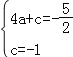
，
解得：
，
∴直线l2的解析式为y=﹣
x﹣1，
∵l1、l2相交于点D，
∴点D的坐标是方程组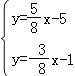
的解
练习册系列答案
阅读快车系列答案
相关题目
