题目内容
【题目】在△ABC中,AB=AC,点E,F分别在AB,AC的延长线上,AE=AF,BF与CE相交于点P,求证:PB=PC,并请直接写出图中其他相等的线段.
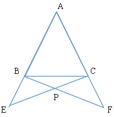
【答案】证明见解析,BF=CE,PF=PE,BE=CF.
【解析】
试题分析:本题考查了全等三角形的判定和性质以及等腰三角形的性质,是基础题,难度不大.可证明△ABF≌△ACE,则∠ABF=∠ACE,可进一步得到∠PBC=∠PCB,可证明PB=PC,从而可得出BF=CE,PF=PE,BE=CF.
试题解析:∵AB=AC,
∴∠ABC=∠ACB,
又∵AE=AF,∠A=∠A,
∴ΔABF≌ΔACE(SAS),
∴∠ABF=∠ACE,
∴∠ABF-∠ABC=∠ACE-∠ACB,
即∠PBC=∠PCB,
∴PB=PC,
相等的线段还有BF=CE,PF=PE,BE=CF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目