Question

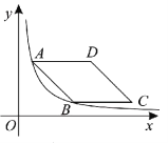
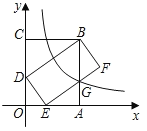
【题目】如图，矩形OABC的顶点A、C分别在x轴、y轴的正半轴上，点D在边OC上，且BD=OC，以BD为边向下作矩形BDEF，使得点E在边OA上，反比例函数y(k≠0)的图象经过边EF与AB的交点G．若AG，DE=2，则k的值为____．

Answer 1

【答案】．

【解析】

如图，连接DF，BE，由“HL”可证Rt△BDE≌Rt△BAE，可得AE=DE=2，由勾股定理可求EG，通过证明△DEO∽△EGA，可得，可求OE的长，即可求点G坐标，代入解析式可求k的值．

如图，连接DF，BE，

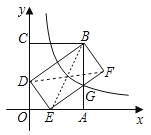
∵四边形OABC是矩形，四边形BDEF是矩形，

∴OC=AB，BE=DF，∠BAO=∠BDE=∠DEF=90°．

∵BD=OC，∴BD=AB，

又∵BE=BE，

∴Rt△BDE≌Rt△BAE(HL)，

∴AE=DE=2，

∴EG，

∵∠DEO+∠AEG=90°，∠EDO+∠DEO=90°，

∴∠AEG=∠EDO，

又∵∠EOD=∠EAG=90°，

∴△DEO∽△EGA，

∴，

∴，

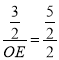∴OE，

∴OA=2，

∴点G(，)．

∵反比例函数y(k≠0)的图象经过点G，

∴k．

故答案为：．