Question

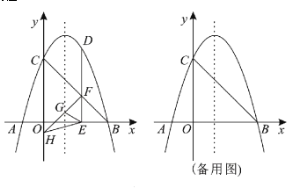
【题目】在ABCD中，AF平分∠BAD交BC于点F，∠BAC=90°，点E是对角线AC上的点，连结BE．

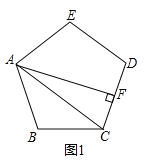
（1）如图1，若AB=AE，BF=3，求BE的长；

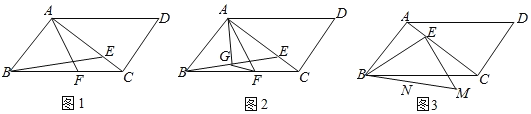
（2）如图2，若AB=AE，点G是BE的中点，∠FAG=∠BFG，求证：ABFG；

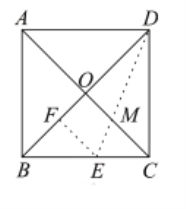
（3）如图3，以点E为直角顶点，在BE的右下方作等腰直角△BEM，若点E从点A出发，沿AC运动到点C停止，设在点E运动过程中，BM的中点N经过的路径长为m，AC的长为n，请直接写出的值．

Answer 1

【答案】（1）BE=3；（2）证明见解析；（3）．

【解析】

（1）先说明AB=BF，然后再利用等腰直角三角形的性质求解即可；

（2）如图2：连接EF，过点G作GH⊥EF交EF的延长线于H．设BG=a，FG=b．先利用相似三角形的性质证得EFGF，最后根据解直角三角形求得AB即可；

（3）如图3：在AC上取一点T，使得AT=AB，连接BT，TM，取BT的中点J，连接NJ．

先证NJ//TM，NJ=TM，得到∠BJN=∠BTM=90°，进一步得到点N的运动轨边是线段，最后代入即可．

解：（1）如图1中，

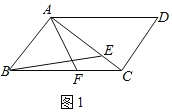
∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠DAF=∠AFB

∵AF平分∠BAD，

∴∠DAF=∠BAF，

∴∠BAF=∠AFB，

∴AB=BF=3．

∵AB=AE，∠BAE=90°，

∴BEAB=3．

（2）连接EF，过点G作GH⊥EF交EF的延长线于H．设BG=a，FG=b．

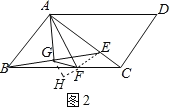
∵AB=AE，∠BAE=90°，BG=GE，

∴AG⊥BE，AG=GB=GE，

∴ABBGa．

∵BF=ABa，

∴BF2=2a2，BGBE=2a2，

∴BF2=BGBE，

∴，

∵∠FBG=∠EBF，

∴△GBF∽△FBE，

∴，∠BFG=∠BEF，

∴EFGFb．

∵∠BAF=∠BFA，∠GAF=∠BFG，

∴∠AFG=∠BAG=45°，∠GAF=∠GEF，

∴∠AGE=∠AFE=90°，

∴∠GFH=45°．

∵GH⊥EH，

∴GH=FHb，

∴EH=FH+EFb，

∴EGb

∴AB=AEGEb，

∴ABGF．

（3）如图3中，在AC上取一点T，使得AT=AB，连接BT，TM，取BT的中点J，连接NJ．

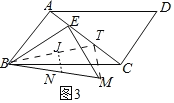
∵△ABT，△BEM都是等腰直角三角形，

∴BTAB，BMBE，∠ABT=∠EBM=45°，

∴，∠ABE=∠TBM，

∴△ABE∽△TBM，

∴，∠AEB=∠BMT．

∵∠AEB+∠BET=180°，

∴∠BMT+∠BET=180°，

∴∠EBM+∠ETM=180°．

∵∠EBM=∠ETB=45°，

∴∠ETM=135°，∠BTM=90°．

∵BJ=JT，BN=NM，

∴NJ∥TM，NJTM，

∴∠BJN=∠BTM=90°，

∴点N的运动轨迹是线段JN，JNTMAE．

∵点E从A运动到C时，AE=AC=n，

∴mn，

∴．