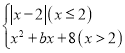题目内容
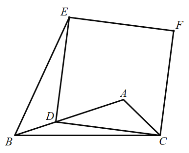
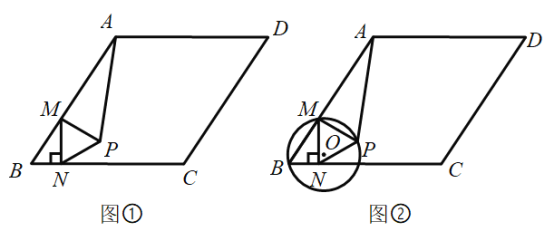
【题目】如图①,在菱形![]() 中
中![]() ,
,![]() ,边
,边![]() 上一动点
上一动点![]() 从点
从点![]() 出发向点
出发向点![]() 匀速运动,速度为
匀速运动,速度为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,以
,以![]() 为边长作等边
为边长作等边![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的异侧,连接
的异侧,连接![]() .点
.点![]() 的运动时间为
的运动时间为![]() .
.
(1)当![]() 时,
时,![]() _______
_______![]() ;(直接写出答案)
;(直接写出答案)
(2)连接![]() ,若
,若![]() 为等腰三角形,求
为等腰三角形,求![]() 的值;
的值;
(3)如图②,经过点![]() 、
、![]() 、
、![]() 作
作![]() ,连接
,连接![]() ,当
,当![]() 与
与![]() 相切时,则
相切时,则![]() 的值等于_______
的值等于_______![]() (直接写出答案)
(直接写出答案)
【答案】(1)![]() ;(2)当
;(2)当![]() ,
,![]() 秒时,
秒时,![]() 为等腰三角形;(3)当
为等腰三角形;(3)当![]() 与
与![]() 相切时,则
相切时,则![]()
【解析】
(1)当![]() 时,BM=4,AM=6,在Rt△BMN中解直角三角形求得MN;再根据等边三角形的性质得到MP=MN,然后再说明∠AMP=90°,最后在Rt△APM运用勾股定理解答即可.
时,BM=4,AM=6,在Rt△BMN中解直角三角形求得MN;再根据等边三角形的性质得到MP=MN,然后再说明∠AMP=90°,最后在Rt△APM运用勾股定理解答即可.
(2)先说明![]() 、
、![]() ,再在
,再在![]() 中解三角形用t表示出AP,最后分PA=PB、PB=BA、PA=AB三种情况分别求解即可;
中解三角形用t表示出AP,最后分PA=PB、PB=BA、PA=AB三种情况分别求解即可;
(3)设BP的中点为O点,连接MD.先说明∠BMO=∠DMP;然后再延长AB,过D作DE⊥AE,交于E点.可得DE//MP,进一步说明∠EDM=∠BMO;再证△BMP∽△DEM,最后运用相似三角形的性质解答即可.
解:(1)当![]() 时,BM=4,AM=6
时,BM=4,AM=6
∵![]() ,
,![]() ,
,![]()
∴MN=BM·sin∠ABC=4×![]() =2
=2![]() ,∠NMN=30°
,∠NMN=30°
∴∠AMP=90°
∵![]() 是等边三角形
是等边三角形
∴MP=MN=2![]()
在Rt△APM中,运用勾股定理得:
AP=![]()
故答案为4![]() .
.
(2)如图:连接BP
![]() ,
,![]() ,
,![]()
![]()
![]()
![]() 等边
等边![]()
![]() ,
,![]()
![]()
![]() 在
在![]() 中
中![]()
在![]() 中
中![]() ,
,![]()
![]() .
.
①若![]() 即
即![]()
![]() 则
则![]() (秒)
(秒)
②若![]() 即
即![]()
![]() (秒)
(秒)
③若![]() 即
即![]()
则![]()
![]() (舍),
(舍),![]() (舍)
(舍)
综上所述:当![]() ,
,![]() 秒时,
秒时,![]() 为等腰三角形.
为等腰三角形.
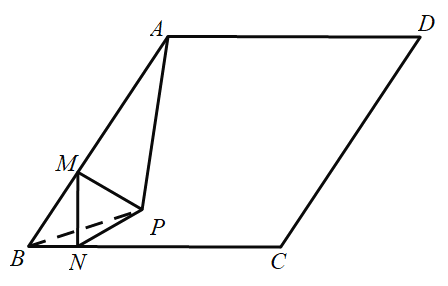
(3)设BP的中点为O点,连接MD.
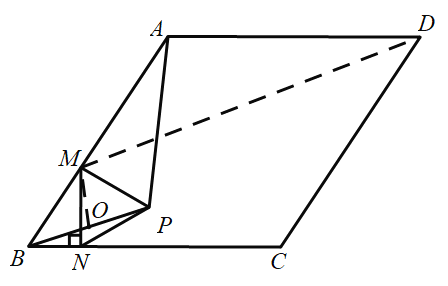
∵MD与圆0相切
∴MO⊥MD
∴∠DMO=∠BMP=90°
∴∠BMO=∠DMP,
延长AB,过D作DE⊥AE,交于E点
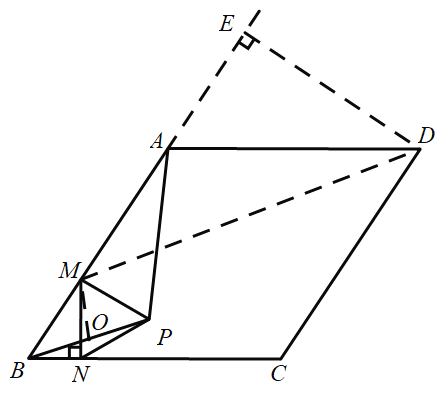
∴DE//MP,
∴∠EDM=∠DMP
∴∠EDM=∠BMO,
在△BMO中,BO=MO,
∴∠MBO =∠BMO,
∴∠EDM=∠BMO,
∴△BMP∽△DEM,
∴![]()
在Rt△ADE中,AD= 10,∠EAD=60°,
∵AE = 5,DE=5![]()
∴ME = 15-2t,
∴![]()
解得t1=![]() ,t2=0,
,t2=0,
∵t>0,
∴t=![]()
∴当![]() 与
与![]() 相切时,则
相切时,则![]() .
.

 小学教材完全解读系列答案
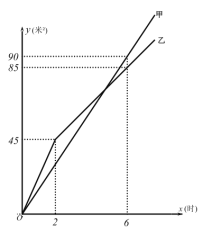
小学教材完全解读系列答案【题目】某社区为了加强社区居民对新型冠状病非肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取![]() 名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:![]()
![]()
乙小区:![]()
![]()
整理数据
成绩 |
|
|
|
|
甲小区 |
|
|
|
|
乙小区 |
|
|
|
|
分析数据
统计量 | 平均数 | 中位教 | 众数 |
甲小区 |
|
|
|
乙小区 |
|
|
|
应用数据
(1)填空:![]() _ _;
_ _;
(2)若甲小区共有![]() 人参与答卷,请估计甲小区成绩大于
人参与答卷,请估计甲小区成绩大于![]() 分的人数;
分的人数;
(3)社区管理员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理员的理由(至少写出一条) .