题目内容
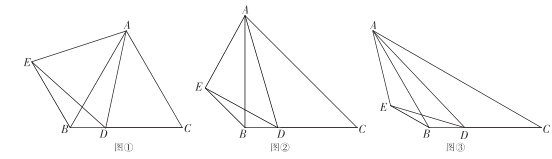
【题目】如图,在△ABC中, AB=AC,D 为 BC 边上任意一点,以AD为底边向左侧作等腰△ADE,∠AED=∠ABC ,连接![]() .
.
(1)如图 ① ,当∠ABC=60°时,易证:CD=BE(不需要证明);
(2)当∠ABC=90°时,如图 ② ;当∠ABC=120°时,如图 ③ ;线段CD和BE又有怎样的关系? 并选择一个图形证明你的结论.
【答案】(1)见解析;(2)图②的结论是:![]() ;图 ③ 的结论是:
;图 ③ 的结论是:![]() ,证明过程见解析.
,证明过程见解析.
【解析】
(1)△EAD为等腰三角形,当∠ABC=60°=∠AED时,可推出△AED为等边三角形,进一步证明△AEB≌△ADC,即得到CD=BE;
(2)当∠ABC=90°=∠AED时,此时△AED、△ABC变成等腰直角三角形,∴∠EAD=∠BAC=45°,可推出∠EAB=∠DAC,且![]() ,故可证明△AEB∽△ADC,即可得到
,故可证明△AEB∽△ADC,即可得到![]() ;
;
当∠ABC=120°=∠AED时,此时△AED、△ABC变成30°、30°、120°的等腰三角形,同样可证明△AEB∽△ADC,即可得到![]() .
.
解:(1) 证明:∵△EAD为等腰三角形,且∠ABC=60°=∠AED,
∴△AED变成等边三角形,∴∠EAD=∠BAC,
又∠EAB=60°-∠BAD,∠DAC=60°-∠BAD
∴∠EAB=∠DAC,
在△AEB和△ADC中:

∴△AEB≌△ADC,
∴CD=BE.
(2)图②的结论是:![]()
图③的结论是:![]() .
.
下面选择图②进行证明:
证明:![]()
∴△AED,△ABC都是等腰直角三角形,
∴∠CAD+∠DAB=∠EAB+∠BAD=45°
∴∠CAD=∠BAE
![]()
∴△BAE∽△CAD
![]() .
.
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目