题目内容
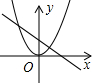
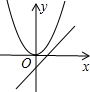
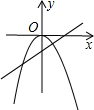
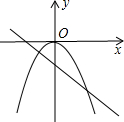
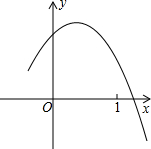
如图二次函数y=ax2+bx+c的顶点在第四象限,且经过点(0,-2)、(-1,0),则y=a+b+c的取值范围是( )

| A.-2<y<0 | B.0<y<2 | C.-4<y<0 | D.0<y<4 |

∵二次函数y=ax2+bx+c(a>0)的图象与坐标轴分别交于点(0,-2)、(-1,0),
∴c=-2,a-b+c=0,
即b=a-2,
∵顶点在第四象限,
∴-
>0,
<0,
又∵a>0,
∴b<0,
∴b=a-2<0,即a<2,
b2-4ac=(a+c)2-4ac=(a-c)2>0
∵a-b+c=0,
∴a+b+c=2b<0,
∴a+b+c=2b=2a-4,
∵0<a<1,
∴a+b+c=2b=2a-4>-4,
∴-4<a+b+c<0.
∴-4<y<0.
故选C.
∴c=-2,a-b+c=0,
即b=a-2,
∵顶点在第四象限,
∴-
| b |
| 2a |
| 4ac-b2 |
| 4a |
又∵a>0,
∴b<0,
∴b=a-2<0,即a<2,
b2-4ac=(a+c)2-4ac=(a-c)2>0
∵a-b+c=0,
∴a+b+c=2b<0,
∴a+b+c=2b=2a-4,
∵0<a<1,
∴a+b+c=2b=2a-4>-4,
∴-4<a+b+c<0.
∴-4<y<0.
故选C.

练习册系列答案
相关题目