��Ŀ����
����Ŀ����ͼ1����֪��B��0��9������CΪx����һ���㣬����BC����ODC�͡�EBC���ǵȱ������Σ�

��1����֤��DE��BO��
��2����ͼ2������Dǡ������BC��ʱ��
�����E�����ꣻ
����x�����Ƿ���ڵ�P��ʹ��PECΪ���������Σ������ڣ�д����P�����ꣻ�������ڣ�˵�����ɣ�
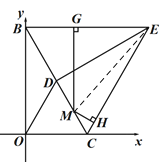
����ͼ3����M���߶�BC�ϵĶ��㣨��B����C���⣩������M��MG��BE�ڵ�G��MH��CE�ڵ�H������M�˶�ʱ��MH��MG��ֵ�Ƿ����仯��������仯��ֱ��д��MH��MG��ֵ������仯����Ҫ˵�����ɣ�
���𰸡���1������������2����E��6![]() ��9�����ڴ��ڣ���P������Ϊ����3
��9�����ڴ��ڣ���P������Ϊ����3![]() ��0����9
��0����9![]() ��0�����۲��仯��MH��MG��9
��0�����۲��仯��MH��MG��9
��������
��1�����ݵȱ������ε����ʵõ�BC=CE��OC=CD����OCD=��BCE=60���������OCB=��DCE������ȫ�������ε����ʼ��ɵõ����ۣ�
��2�����ɵ�B��0��9�����õ�OB=9������ȫ�������ε����ʵõ���CDE=��BOC=90�������ݵȱ������ε����ʵõ���DEC=30�������![]() ����E��EF��x����F���������μ��ɵõ����ۣ�
����E��EF��x����F���������μ��ɵõ����ۣ�
�����ڣ���ͼ����![]() ʱ����CE=PE�����ݵ��������ε����ʼ��ɵõ����ۣ�������仯������EM�����������ε������ʽ���ɵõ����ۣ�
ʱ����CE=PE�����ݵ��������ε����ʼ��ɵõ����ۣ�������仯������EM�����������ε������ʽ���ɵõ����ۣ�
��1���ߡ�ODC����EBC���ǵȱ�������
��OC��DC��BC��CE����OCD����BCE��60��
���BCE����BCD����OCD����BCD
����ECD����BCO
���DEC�ա�OBC��SAS��
��DE��BO
��2���١���B��0��9����
��OB=9��
�ɣ�1��֪��BCO�ա�ECD��
���CDE=��BOC=90����
��DE��BC��
�ߡ�EBC�ǵȱ������Σ�
���DEC=30����
���OBC=��DEC=30����
��![]() ��
��![]() ��
��
��![]() ��
��
��E��EF��x����F��

�ߡ�DCO=��BCE=60����
���ECF=60����
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��E��6![]() ��9����
��9����
�����ڣ���ͼ��

��![]() ʱ��
ʱ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��CE=PE��
�ߡ�ECP=60����
���CPE�ǵȱ������Σ�
��P2��P3�غϣ�
������PECΪ����������ʱ����P������Ϊ����3![]() ��0����9
��0����9![]() ��0����
��0����
������仯����ͼ������EM��
��![]()
��BC=CE=BE��
��GM+MH=DE=9��
��MH+MG��ֵ���ᷢ���仯��

 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�




