题目内容
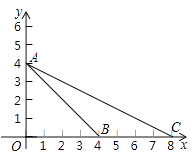
【题目】如图,一次函数y=![]() x﹣2的图象与x轴交于点A,与y轴交于点B,点D的坐标为(﹣1,0),二次函数y=ax2+bx+c(a≠0)的图象经过A,B,D三点.
x﹣2的图象与x轴交于点A,与y轴交于点B,点D的坐标为(﹣1,0),二次函数y=ax2+bx+c(a≠0)的图象经过A,B,D三点.
(1)求二次函数的解析式;
(2)如图1,已知点G(1,m)在抛物线上,作射线AG,点H为线段AB上一点,过点H作HE⊥y轴于点E,过点H作HF⊥AG于点F,过点H作HM∥y轴交AG于点P,交抛物线于点M,当HEHF的值最大时,求HM的长;
(3)在(2)的条件下,连接BM,若点N为抛物线上一点,且满足∠BMN=∠BAO,求点N的坐标.
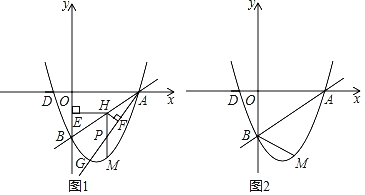
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)2;(3)(1,﹣3)或(﹣
x﹣2;(2)2;(3)(1,﹣3)或(﹣![]() ,
,![]() )
)
【解析】
(1)二次函数经过D(﹣1,0),B(4,0),可以假设二次函数的解析式为y=a(x+1)(x﹣4),把A(0,﹣2)代入得到a=![]() 即可解决问题.
即可解决问题.
(2)如图1中,设H(x0,![]() x0﹣2),且(0≤x0≤4),构建二次函数,利用二次函数的性质即可解决问题.
x0﹣2),且(0≤x0≤4),构建二次函数,利用二次函数的性质即可解决问题.
(3)如图2中,过点B作BT⊥MN于T.由题意BM=![]() ,BT=1,MT=2,设T(m,n),利用两点间距离公式构建方程组求出m,n,再求出直线MN的解析式,构建方程组确定解得N的坐标即可.
,BT=1,MT=2,设T(m,n),利用两点间距离公式构建方程组求出m,n,再求出直线MN的解析式,构建方程组确定解得N的坐标即可.
解:(1)在y=![]() x﹣2中,当x=0时,y=﹣2,当y=0时,x=4,
x﹣2中,当x=0时,y=﹣2,当y=0时,x=4,
∴A(4,0),B(0,﹣2),
∵二次函数经过D(﹣1,0),B(4,0),
∴可以假设二次函数的解析式为y=a(x+1)(x﹣4),
把A(0,﹣2)代入得到a=![]() ,
,
∴二次函数的解析式为y=![]() x2﹣
x2﹣![]() x﹣2.
x﹣2.
(2)如图1中,设H(x0,![]() x0﹣2),且(0≤x0≤4),
x0﹣2),且(0≤x0≤4),
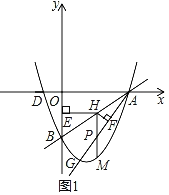
∵HE⊥y轴于E,
∴HE=x0,
∵G(1,m)在抛物线上,
∴G(1,﹣3),
∵A(4,0),
∴直线AG的解析式为y=x﹣4,
∵HM∥y轴交AG于P,
∴P(x0,x0﹣4),则PH=(![]() x0﹣2)﹣(x0﹣4)=﹣
x0﹣2)﹣(x0﹣4)=﹣![]() x0+2,
x0+2,
由直线AG都是解析式y=x﹣4,HM∥y轴交AG于P,可得∠HPF=45°,
∵HF⊥AG于F,
∴HF=![]() (﹣
(﹣![]() x0+2),
x0+2),
∴HEHF=![]() (﹣
(﹣![]() x0+2)x0=﹣
x0+2)x0=﹣![]() x02+
x02+![]() x0=﹣
x0=﹣![]() (x0﹣2)2+
(x0﹣2)2+![]() ,
,
∵﹣![]() <0,0≤x0≤4,
<0,0≤x0≤4,
∴当x0=2时,HEHF的值最大,此时H(2,﹣1),M(2,﹣3),
∴HM=﹣1﹣(﹣3)=2.
(3)如图2中,过点B作BT⊥MN于T.

∵∠BMN=∠BAO,
∴tan∠BMN=tan∠BAO=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
又∵B(0,﹣2),M(2,﹣3),可得BM=![]() ,BT=1,MT=2,
,BT=1,MT=2,
设T(m,n),则 解得
解得![]() 或
或 ,
,
∴T(0,﹣3)或(![]() ,﹣
,﹣![]() ),
),
∵M(2,﹣3),
∴直线MN的解析式为y=﹣3或y=﹣![]() x﹣
x﹣![]() ,
,
联立得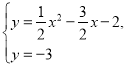 或
或 ,
,
分别解方程组可得![]() 或
或![]() 或
或 或
或![]() ,舍弃第二,第四组解,
,舍弃第二,第四组解,
∴满足条件的点N的坐标为(1,﹣3)或(﹣![]() ,
,![]() ).
).