题目内容
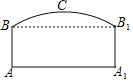
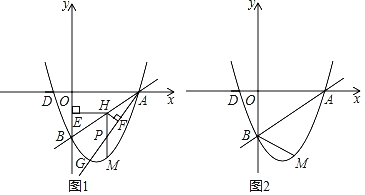
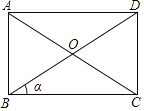
【题目】(1)如图,矩形ABCD的对角线长为a,对角线与一边的夹角为α(α≤45°),则CD= (用α的三角函数和a来表示),S△BCD= (用α的三角函数和a来表示)= (用2α的三角函数和a来表示);
(2)猜想并直接写出sin2α,sinα,cosα之间的数量关系.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据锐角三角函数,可以用α的三角函数和a来表示出CD,然后根据三角形的面积公式和锐角三角函数可以表示出S△BCD,本题得以解决;
(2)先写出sin2α,sinα,cosα之间的数量关系,然后根据(1)中S△BCD的结果,可以说明这个数量关系为什么成立.
解:(1)∵四边形ABCD是矩形,∠DBC=α,AC=a,
∴∠BCD=90°,OA=OC=OB=OD=![]() a,BD=a,
a,BD=a,
∴CD=asinα,BC=acosα,
∴S△BCD=![]() BCCD=
BCCD=![]() ×acosα×asinα=
×acosα×asinα=![]() a2sinαcosα,
a2sinαcosα,
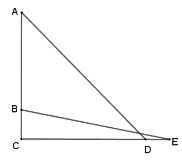
作CE⊥BD于点E,
∵OB=OC,∠OBC=α,
∴∠OBC=∠OCB,
∴∠EOC=2α,
∴EC=OCsin2α=![]() asin2α,
asin2α,
∴S△BCD=![]() BDCE=
BDCE=![]() a
a![]() asin2α=
asin2α=![]() a2sin2α,
a2sin2α,
故答案为:asinα,![]() a2sinαcosα,
a2sinαcosα,![]() a2sin2α;
a2sin2α;
(2)sin2α=2sinαcosα,
理由:∵S△BCD=![]() a2sinαcosα,S△BCD=
a2sinαcosα,S△BCD=![]() a2sin2α,
a2sin2α,
∴![]() a2sinαcosα=
a2sinαcosα=![]() a2sin2α,
a2sin2α,
∴sin2α=2sinαcosα.


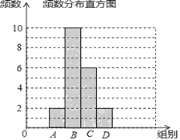
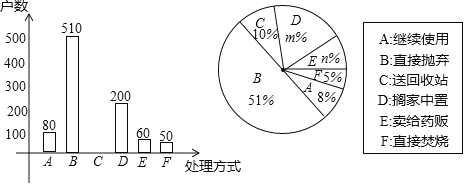
【题目】张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理,绘制了如下不完整的统计图表:
组别 | 步数分组 | 频率 |
A | x<6000 | 0.1 |
B | 6000≤x<7000 | 0.5 |
C | 7000≤x<8000 | m |
D | x≥8000 | n |
合计 | 1 |
根据信息解答下列问题:
(1)填空:m= ,n= ;并补全条形统计图;
(2)这20名朋友一天行走步数的中位数落在 组;(填组别)
(3)张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞,请求出甲、乙被同时点赞的概率.