题目内容
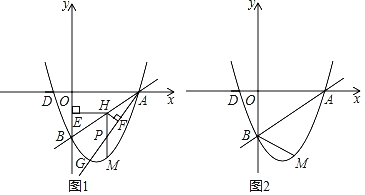
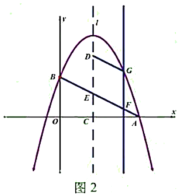
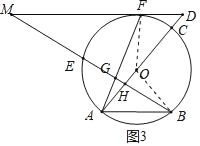
【题目】如图,F为⊙O上的一点,过点F作⊙O的切线与直径AC的延长线交于点D,过圆上的另一点B作AO的垂线,交DF的延长线于点M,交⊙O于点E,垂足为H,连接AF,交BM于点G.
(1)求证:△MFG为等腰三角形.
(2)若AB∥MD,求MF、FG、EG之间的数量关系,并说明理由.
(3)在(2)的条件下,若DF=6,tan∠M=![]() ,求AG的长.
,求AG的长.
【答案】(1)详见解析;(2)FG2=EGMF,理由详见解析;(3)![]() .
.
【解析】
(1)连接OF,由切线的性质结合等角的余角相等可得出∠MFG=∠AGH,进而得出∠MFG=∠MGF,可证出△MFG为等腰三角形;
(2)由MD∥AB可得出∠M=∠B,连接EF,则∠EFG=∠B,进而可得出∠M=∠EFG,结合∠MGF=∠FGE可得出△MGF∽△FGE,利用相似三角形的性质可得出FG2=EGMG,结合MF=MG可得出FG2=EGMF;
(3)由∠M=∠B,tan∠M=![]() ,设AH=3k,则HB=4k,AB=5k,连接FO,OB,由∠MHD=∠OFD=90°,∠D=∠D可得出∠FOD=∠M,结合FD=6,可得出FO=8=OB=OA,进而可得出OH=8﹣3k,在Rt△OHB中,利用勾股定理可求出k值,由MD∥AB可得出∠MFG=∠BAF,进而可得出∠BGA=∠BAG,由等角对等腰可得出AB=GB=5k,结合BH=4k可得出GH=k,结合AH=3k利用勾股定理可求出AG=
,设AH=3k,则HB=4k,AB=5k,连接FO,OB,由∠MHD=∠OFD=90°,∠D=∠D可得出∠FOD=∠M,结合FD=6,可得出FO=8=OB=OA,进而可得出OH=8﹣3k,在Rt△OHB中,利用勾股定理可求出k值,由MD∥AB可得出∠MFG=∠BAF,进而可得出∠BGA=∠BAG,由等角对等腰可得出AB=GB=5k,结合BH=4k可得出GH=k,结合AH=3k利用勾股定理可求出AG=![]() k,再代入k值即可求出结论.
k,再代入k值即可求出结论.
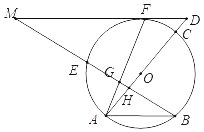
(1)证明:连接OF,如图1所示.
∵DF为⊙O的切线,
∴OF⊥DM,
∴∠MFG+∠AFO=90°.
∵BH⊥AD,
∴∠AHG=90°,
∴∠AGH+∠GAH=90°.
∵OA=OF,
∴∠OAF=∠OFA,
∴∠MFG=∠AGH.
又∵∠MGF=∠AGH,
∴∠MFG=∠MGF,
∴△MFG为等腰三角形.
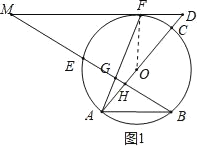
(2)解:FG2=EGMF,理由如下:
∵MD∥AB,
∴∠M=∠B.
连接EF,如图2所示.
∵∠EFG=∠B,
∴∠M=∠EFG.
又∵∠MGF=∠FGE,
∴△MGF∽△FGE,
∴![]() ,即FG2=EGMG,
,即FG2=EGMG,
∴FG2=EGMF.
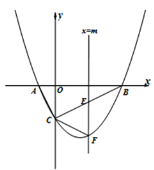
(3)解:∵∠M=∠B,tan∠M=![]() ,
,
∴设AH=3k,则HB=4k,AB=5k.
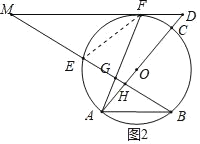
连接FO,OB,如图3所示.
∵∠MHD=∠OFD=90°,∠D=∠D,
∴∠FOD=∠
∵FD=6,
∴FO=8=OB=OA,
∴OH=8﹣3k.
在Rt△OHB中,OH2+HB2=OB2,即(4k)2+(8﹣3k)2=82,
解得:k=![]() .
.
∵MD∥AB,
∴∠MFG=∠BAF,
∴∠BGA=∠BAG,
∴AB=GB=5k,
∴GH=k,
∴AG=![]() k,(勾股定理)
k,(勾股定理)
∴AG=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理,绘制了如下不完整的统计图表:
组别 | 步数分组 | 频率 |
A | x<6000 | 0.1 |
B | 6000≤x<7000 | 0.5 |
C | 7000≤x<8000 | m |
D | x≥8000 | n |
合计 | 1 |
根据信息解答下列问题:
(1)填空:m= ,n= ;并补全条形统计图;
(2)这20名朋友一天行走步数的中位数落在 组;(填组别)
(3)张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞,请求出甲、乙被同时点赞的概率.