题目内容
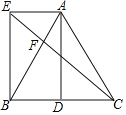
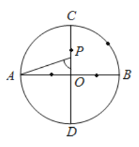
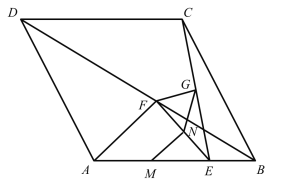
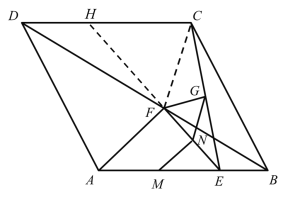
【题目】如图,菱形![]() 的边长为1,
的边长为1,![]() ,点E是边
,点E是边![]() 上任意一点(端点除外),线段
上任意一点(端点除外),线段![]() 的垂直平分线交
的垂直平分线交![]() ,
,![]() 分别于点F,G,
分别于点F,G,![]() ,
,![]() 的中点分别为M,N.
的中点分别为M,N.
(1)求证:![]() ;
;
(2)求![]() 的最小值;
的最小值;
(3)当点E在![]() 上运动时,
上运动时,![]() 的大小是否变化?为什么?
的大小是否变化?为什么?
【答案】(1)见解析;(2)![]() ;(3)不变,理由见解析.
;(3)不变,理由见解析.
【解析】
(1)连接CF,根据垂直平分线的性质和菱形的对称性得到CF=EF和CF=AF即可得证;
(2)连接AC,根据菱形对称性得到AF+CF最小值为AC,再根据中位线的性质得到MN+NG的最小值为AC的一半,即可求解;
(3)延长EF,交DC于H,利用外角的性质证明∠AFC=∠FCE+∠FEC+∠FAE+∠FEA,再由AF=CF=EF,得到∠AEF=∠EAF,∠FEC=∠FCE,从而推断出∠AFD=∠FAE+∠ABF=∠FAE+∠CEF,从而可求出∠ABF=∠CEF=30°,即可证明.
解:(1)连接CF,
∵FG垂直平分CE,
∴CF=EF,
∵四边形ABCD为菱形,
∴A和C关于对角线BD对称,
∴CF=AF,
∴AF=EF;
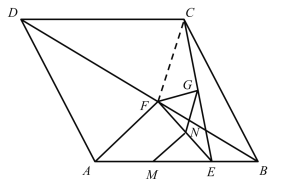
(2)连接AC,
∵M和N分别是AE和EF的中点,点G为CE中点,
∴MN=![]() AF,NG=
AF,NG=![]() CF,即MN+NG=
CF,即MN+NG=![]() (AF+CF),
(AF+CF),
当点F与菱形ABCD对角线交点O重合时,
AF+CF最小,即此时MN+NG最小,
∵菱形ABCD边长为1,∠ABC=60°,
∴△ABC为等边三角形,AC=AB=1,
即MN+NG的最小值为![]() ;
;
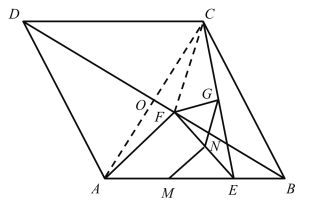
(3)不变,理由是:
延长EF,交DC于H,
∵∠CFH=∠FCE+∠FEC,∠AFH=∠FAE+∠FEA,
∴∠AFC=∠FCE+∠FEC+∠FAE+∠FEA,
∵点F在菱形ABCD对角线BD上,根据菱形的对称性可得:
∠AFD=∠CFD=![]() ∠AFC,
∠AFC,
∵AF=CF=EF,
∴∠AEF=∠EAF,∠FEC=∠FCE,
∴∠AFD=∠FAE+∠ABF=∠FAE+∠CEF,
∴∠ABF=∠CEF,
∵∠ABC=60°,
∴∠ABF=∠CEF=30°,为定值.

【题目】某公园的门票价格如表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
现某单位要组织其市场部和生产部的员工游览该公园,这两个部门人数分别为a和b(a≥b).若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则共需支付门票费为990元,那么这两个部门的人数a=_____;b=_____.
【题目】2020年是脱贫攻坚年,为实现全员脱贫目标,某村贫困户在当地政府支持帮助下,办起了养鸡场,经过一段时间精心饲养,总量为3000只的一批鸡可以出售.现从中随机抽取50只,得到它们质量的统计数据如下:
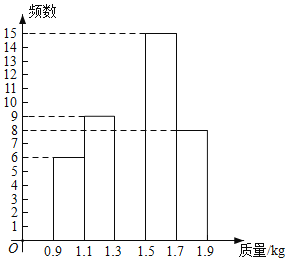
质量 | 组中值 | 数量(只) |
| 1.0 | 6 |
| 1.2 | 9 |
| 1.4 | a |
| 1.6 | 15 |
| 1.8 | 8 |
根据以上信息,解答下列问题:
(1)表中![]() ______,补全频数分布直方图;
______,补全频数分布直方图;
(2)这批鸡中质量不小于![]() 的大约有多少只?
的大约有多少只?
(3)这些贫因户的总收入达到54000元,就能实现全员脱贫目标.按15元![]() 的价格售出这批鸡后,该村贫困户能否脱贫?
的价格售出这批鸡后,该村贫困户能否脱贫?