题目内容
【题目】如图,在平面直角坐标系中, ![]() ,
, ![]() 两点的坐标分别为
两点的坐标分别为![]() ,
, ![]() ,连接
,连接![]() ,若以点
,若以点![]() ,
, ![]() ,
, ![]() 为顶点的三角形是等腰直角三角形,则点
为顶点的三角形是等腰直角三角形,则点![]() 坐标为__________.
坐标为__________.

【答案】![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
【解析】∵A、B两点的坐标分别为(-4,0)、(0,2)
∴OA=4,OB=2.
(1)如图,当∠APB=90°时,作PE⊥OA于点E,
易证△APE≌△BPD,则PD=PE=OE=OD,AE=BD,
设PD= ![]() ,
,
则![]() ,解得:
,解得: ![]() ,
,
∴此时点P的坐标为(-3,3);
同理可得:点P1的坐标为(-1,-1).
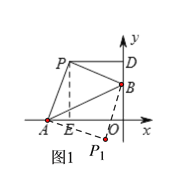
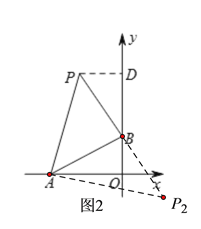
(2)如图2,当∠ABP=90°时,作PD⊥OB于点D,
易证△ABO≌△BPD,则PD=OB=2,BD=AO=4,
∴OD=OB+BD=6,
∴点P的坐标为(-2,6).
同理可得P2的坐标为(2,-2).
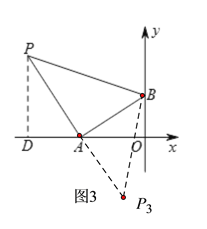
(3)如图3,过点P作PD⊥OA于点D,
易证△PDA≌△AOB,则AD=BO=2,PD=AO=4,
∴OD=AD+OA=6,
∴点P的坐标为(-6,4).
同理可得点P3的坐标为(-2,-4).
综上所述,若△PAB为等腰直角三角形,则点P的坐标为:(-3,3)、(-1,-1)、(-2,6)、(2,-2)、(-6,4)和(-2,-4).

 名校课堂系列答案
名校课堂系列答案【题目】据宜昌市统计局2013年底统计,中心城区人均住房建筑面积约为30平方米,为把宜昌市建设成特大城市,中心城区住房建筑面积和人口数都迅速增加.2014年中心城区住房建筑面积比2013年中心城区住房建筑面积增长的百分数是a,2015年中心城区住房建筑面积比2013年中心城区住房建筑面积增长的百分数是2a.从2014年开始,中心城区人口数在2013年180万的基础上每年递增m(m>0)万人,这样2015年中心城区的人口数比2014年中心城区人口数的1.5倍少80万人,已知2015年中心城区的人均住房建筑面积与2014年持平.
(1)根据题意填表(用含a,m的式子表示各个数量);
年份 | 中心城区人口数 | 中心城区人均住房建筑面积(单位:平方米) | 中心城区住房建筑面积(单位:万平凡米) |
2013年 | 180 | 30 | 5400 |
2014年 |
|
|
|
2015年 |
|
|
|
(2)求题目中的a和m.