题目内容
【题目】在数学课上,老师给出这样一个问题:
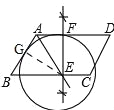
如图1,在平行四边形ABCD中,AB<BC.利用尺规作图,在边BC上确定一点E为圆心作圆,使⊙E与边AB,AD都相切(不写作法,保留作图痕迹);
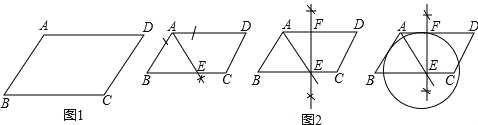
小刚是这样思考的:(如图2)
(1)作∠BAD的平分线与BC边交于点E;
(2)过点E作边AD的垂线,垂足为点F;
(3)以点E为圆心,EF长为半径作圆即可;
小刚把想法和老师交流了,得到了老师的肯定和赞扬,请你回答:小刚这样做的依据是 .
【答案】角平分线上的点到角的两边的距离相等.
【解析】
试题分析:先由作法得出AD与⊙E相切,再根据角平分线上的点到角的两边的距离相等判断出AB也与⊙E相切. 如图,过E作EG⊥AB于G,∵AE平分∠BAD,FE⊥AD,∴EG=EF,∵EF是⊙E的半径,∴AB与⊙E相切.
故答案为:角平分线上的点到角的两边的距离相等.

练习册系列答案
相关题目