题目内容
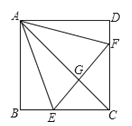
【题目】如图,已知在正方形![]() 中,点
中,点![]() 分别在
分别在![]() 上,△
上,△![]() 是等边三角形,连接
是等边三角形,连接![]() 交
交![]() 于
于![]() ,给出下列结论:
,给出下列结论:
①![]() ; ②
; ② ![]() ;
;
③![]() 垂直平分
垂直平分![]() ; ④
; ④![]() .
.
其中结论正确的共有( ).
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】试题解析:∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴①说法正确;
∵BC=DC,
∴BC-BE=CD-DF,
∴CE=CF,
∴△ECF是等腰直角三角形,
∴∠CFE=45°,
∴∠AFD=75°,
∴∠DAF=15°,
∴②正确;
∵AC是正方形ABCD的对角线,∴∠BCA=45°,
∴AC⊥EF,
又CE=CF,
∴AC垂直平分EF,
∴③正确;
在AD上取一点G,连接FG,使AG=GF,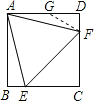
则∠DAF=∠GFA=15°,
∴∠DGF=2∠DAF=30°,
设DF=1,则AG=GF=2,DG=![]() ,
,
∴AD=CD=![]() ,CF=CE=CD-DF=
,CF=CE=CD-DF=![]() ,
,
∴![]() ,而BE+DF=2,
,而BE+DF=2,
∴④说法错误;
综上所述,正确的个数有3个.故本题应选C.

练习册系列答案
相关题目