题目内容
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°. 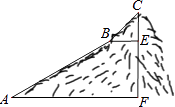
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.( ![]() 1.414,CF结果精确到米)
1.414,CF结果精确到米)
【答案】
(1)解:作BH⊥AF于H,如图,
在Rt△ABH中,∵sin∠BAH= ![]() ,
,
∴BH=800sin30°=400,
∴EF=BH=400m
(2)解:在Rt△CBE中,∵sin∠CBE= ![]() ,
,
∴CE=200sin45°=100 ![]() ≈141.4,
≈141.4,
∴CF=CE+EF=141.4+400≈541(m).
答:AB段山坡高度为400米,山CF的高度约为541米.
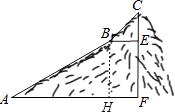
【解析】(1)作BH⊥AF于H,如图,在Rt△ABH中根据正弦的定义可计算出BH的长,从而得到EF的长;(2)先在Rt△CBE中利用∠CBE的正弦计算出CE,然后计算CE和EF的和即可.
【考点精析】根据题目的已知条件,利用关于坡度坡角问题的相关知识可以得到问题的答案,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.

 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案【题目】函数y=x2+3x+2的图象如图1所示,根据图象回答问题: 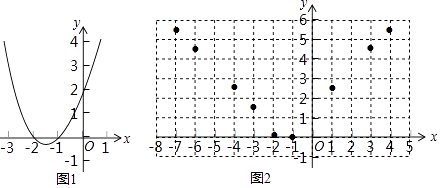
(1)当x时,x2+3x+2>0;
(2)在上述问题的基础上,探究解决新问题: ①函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
②如表是函数y= ![]() 的几组y与x的对应值.
的几组y与x的对应值.
x | … | ﹣7 | ﹣6 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 3 | 4 | … |
y | … | 5.477… | 4.472… | 2.449… | 1.414… | 0 | 0 | 1.414… | 2.449… | 4.472… | 5.477… | … |
如图2,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点的大概位置,请你根据描出的点,画出该函数的图象:
③写出该函数的一条性质: .