题目内容
【题目】在如图的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4. 
(1)试在图中做出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(﹣3,5),试在图中画出平面直角坐标系,并标出A、C两点的坐标;
(3)根据(2)的坐标系,以B为位似中心,做△BA2C2 , 使△BA2C2与△ABC位似,且△BA2C2与△ABC位似比为2:1,并直接写出A2的坐标. 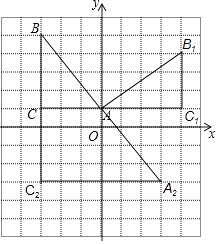
【答案】
(1)解:如图所示:△AB1C1,即为所求
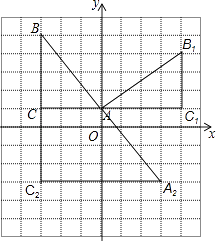
(2)解:如图所示:A(0、1)、C(﹣3、1)

(3)解:如图所示:△BA2C2,即为所求,A2(3、﹣3 )
【解析】(1)直接利用旋转的性质得出对应点位置进而得出答案;(2)利用B点坐标得出原点位置,进而得出A、C两点的坐标;(3)利用位似图形的性质得出对应点位置,进而得出答案.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对作图-位似变换的理解,了解对应点到位似中心的距离比就是位似比,对应线段的比等于位似比,位似比也有顺序;已知图形的位似图形有两个,在位似中心的两侧各有一个.位似中心,位似比是它的两要素.

练习册系列答案
相关题目