题目内容
如图，点C、D在线段AB上，△PCD是等边三角形．
（1）当AC、CD、DB满足怎样的关系时，△ACP∽△PDB？
（2）当△ACP∽△PDB时，求∠APB的度数．
略解析:
解：（1）若△ACP∽△PDB，则有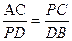
，而PD=PC=CD
∴
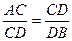∴CD2="AC" DB
故当AC、CD、DB满足CD2="AC" DB时，△ACP∽△PDB
（2）∵△ACP∽△PD ∴A=∠DPB ∴∠A+∠B=∠DPB+∠B=∠PDA="600" ∴∠APB=1200
解：（1）若△ACP∽△PDB，则有
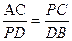，而PD=PC=CD∴
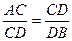∴CD2="AC" DB故当AC、CD、DB满足CD2="AC" DB时，△ACP∽△PDB
（2）∵△ACP∽△PD ∴A=∠DPB ∴∠A+∠B=∠DPB+∠B=∠PDA="600" ∴∠APB=1200
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
25、如图，点C、D在线段AB上，△PCD是等边三角形．
13、如图，点D，E分别在线段AB，AC上，BE，CD相交于点O，AE=AD，要使△ABE≌△ACD，需添加一个条件是
（2013•郴州）如图，点D、E分别在线段AB，AC上，AE=AD，不添加新的线段和字母，要使△ABE≌△ACD，需添加的一个条件是
如图，点C，D在线段AB上，AC=
如图，点C、D在线段AB上，