题目内容
如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.

(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,CT=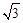 ,求AD的长.
,求AD的长.
【答案】
解:(1)证明:连接OT,
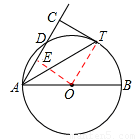
∵OA=OT,∴∠OAT=∠OTA。
又∵AT平分∠BAD,∴∠DAT=∠OAT。∴∠DAT=∠OTA。
∴OT∥AC。
又∵CT⊥AC,∴CT⊥OT。
∵OT是⊙O的半径,∴CT为⊙O的切线。
(2)过O作OE⊥AD于E,则E为AD中点,
∵CT⊥AC,∴OE∥CT。∴四边形OTCE为矩形。
∵CT=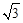 ,∴OE=
,∴OE=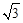 。
。
又∵OA=2,
∴在Rt△OAE中,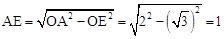 。
。
∴AD=2AE=2。
【解析】
试题分析:(1)连接OT,根据角平分线的性质,以及直角三角形的两个锐角互余,证得CT⊥OT,CT为⊙O的切线。
(2)证明四边形OTCE为矩形,求得OE的长,在直角△OAE中,利用勾股定理即可求解。

练习册系列答案
相关题目
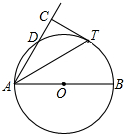 如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.
如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C. 如图,AB是⊙O直径,BC是弦,OD⊥BC于E交弧BC于D.根据中考改编
如图,AB是⊙O直径,BC是弦,OD⊥BC于E交弧BC于D.根据中考改编 如图,AB是⊙O直径,C、D是⊙O上的两点,若∠BAC=20°,
如图,AB是⊙O直径,C、D是⊙O上的两点,若∠BAC=20°,
 如图,AB是⊙O直径,OB=6,弦CD=10,则弦心距OP的长为( )
如图,AB是⊙O直径,OB=6,弦CD=10,则弦心距OP的长为( )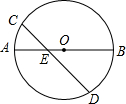 如图,AB是⊙O直径,弦CD交AB于E,∠AEC=45°,AB=2.设AE=x,CE2+DE2=y.下列图象中,能表示y与x的函数关系是的( )
如图,AB是⊙O直径,弦CD交AB于E,∠AEC=45°,AB=2.设AE=x,CE2+DE2=y.下列图象中,能表示y与x的函数关系是的( )