题目内容
如图，AB是⊙O直径，OB=6，弦CD=10，则弦心距OP的长为（ ）分析：连接OD，则OD=OB=6，根据垂径定理求出DP，根据勾股定理求出OP即可．
解答：解：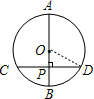
连接OD，则OD=OB=6，
∵AB⊥CD，AB过O，
∴DP=CP=
CD，
∵CD=10，
∴DP=5，
在Rt△DPO中，由勾股定理得：OP=
=
=
，
故选D．
连接OD，则OD=OB=6，
∵AB⊥CD，AB过O，
∴DP=CP=
| 1 |
| 2 |
∵CD=10，
∴DP=5，
在Rt△DPO中，由勾股定理得：OP=
| OD2-DP2 |
| 62-52 |
| 11 |
故选D．
点评：本题考查了垂径定理和勾股定理的应用，关键是构造直角三角形和求出PD长．
练习册系列答案
相关题目
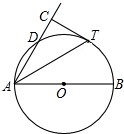如图，AB是⊙O直径，D为⊙O上一点，AT平分∠BAD交⊙O于点T，过T作AD的垂线交AD的延长线于点C．
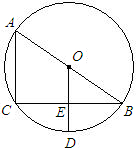如图，AB是⊙O直径，BC是弦，OD⊥BC于E交弧BC于D．根据中考改编
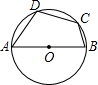如图，AB是⊙O直径，C、D是⊙O上的两点，若∠BAC=20°，
如图，AB是⊙O直径，弦CD交AB于E，∠AEC=45°，AB=2．设AE=x，CE2+DE2=y．下列图象中，能表示y与x的函数关系是的（ ）