题目内容
 如图,AB是⊙O直径,弦CD交AB于E,∠AEC=45°,AB=2.设AE=x,CE2+DE2=y.下列图象中,能表示y与x的函数关系是的( )
如图,AB是⊙O直径,弦CD交AB于E,∠AEC=45°,AB=2.设AE=x,CE2+DE2=y.下列图象中,能表示y与x的函数关系是的( )分析:过点O作OP⊥CD于点P,连接OD,先根据垂径定理得出CP=DP,再由∠OEP=∠AEC=45°,得出OP=PE.设DP=a,PE=b,在Rt△DOP中,运用勾股定理得出a2+b2=R2=1,进而得到CE2+DE2=2(a2+b2)=2,则y=2,即可得出正确选项.
解答: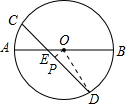 解:过点O作OP⊥CD于点P,连接OD,则CP=DP.
解:过点O作OP⊥CD于点P,连接OD,则CP=DP.
∵∠OEP=∠AEC=45°,
∴OP=PE.
设DP=a,PE=b,则CP=a,OP=b,
∴ED=a+b,EC=a-b.
在Rt△DOP中,OP2+DP2=OD2,
∴a2+b2=R2=1,
∴CE2+DE2=(a-b)2+(a+b)2=2(a2+b2)=2R2=2,
∴y=2,即y的值为一个常数,不随x的值的变化而变化.
故选A.
 解:过点O作OP⊥CD于点P,连接OD,则CP=DP.
解:过点O作OP⊥CD于点P,连接OD,则CP=DP. ∵∠OEP=∠AEC=45°,
∴OP=PE.
设DP=a,PE=b,则CP=a,OP=b,
∴ED=a+b,EC=a-b.
在Rt△DOP中,OP2+DP2=OD2,
∴a2+b2=R2=1,
∴CE2+DE2=(a-b)2+(a+b)2=2(a2+b2)=2R2=2,
∴y=2,即y的值为一个常数,不随x的值的变化而变化.
故选A.
点评:本题考查了动点问题的函数图象,正确作出辅助线,得出CE2+DE2=2R2(R是圆的半径)是解题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
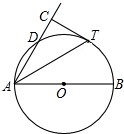 如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.
如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.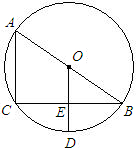 如图,AB是⊙O直径,BC是弦,OD⊥BC于E交弧BC于D.根据中考改编
如图,AB是⊙O直径,BC是弦,OD⊥BC于E交弧BC于D.根据中考改编 如图,AB是⊙O直径,C、D是⊙O上的两点,若∠BAC=20°,
如图,AB是⊙O直径,C、D是⊙O上的两点,若∠BAC=20°,
 如图,AB是⊙O直径,OB=6,弦CD=10,则弦心距OP的长为( )
如图,AB是⊙O直径,OB=6,弦CD=10,则弦心距OP的长为( )