题目内容
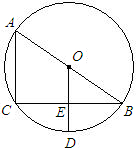 如图,AB是⊙O直径,BC是弦,OD⊥BC于E交弧BC于D.根据中考改编
如图,AB是⊙O直径,BC是弦,OD⊥BC于E交弧BC于D.根据中考改编(1)请写出四个不同类型的正确结论;
(2)连接CD、DB设∠CDB=α,∠ABC=β,你认为α=β+90°这个结论正确吗?若正确请证明过程.若不正确请说明理由.
分析:(1)可根据直径所对的圆周角是90°,得到∠C=90°,利用垂径定理可知OD垂直平分BC并且平分弦所对的弧,即可写出4个结论(可从线段的位置关系,数量关系,弧长之间的关系,角的度数等来写出正确结论).
(2)先根据圆内接四边形的性质找到α与∠A之间的数量关系,再根据直角三角形的性质找到∠A和β之间的数量关系,等量代换化简后即可得到α和β之间的数量关系.
(2)先根据圆内接四边形的性质找到α与∠A之间的数量关系,再根据直角三角形的性质找到∠A和β之间的数量关系,等量代换化简后即可得到α和β之间的数量关系.
解答: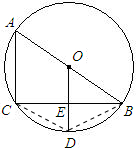 解:(1)OD∥AC、∠C=90°、CE=BE、OE=
解:(1)OD∥AC、∠C=90°、CE=BE、OE=
AC、
=
.
(2)α=β+90°正确.
∵ACDB是圆内接四边形
∴α=180°-∠A
∵∠A=90°-β
∴α=180°-(90°-β)=β+90°.
 解:(1)OD∥AC、∠C=90°、CE=BE、OE=
解:(1)OD∥AC、∠C=90°、CE=BE、OE=| 1 |
| 2 |
 |
| CD |
 |
| BD |
(2)α=β+90°正确.
∵ACDB是圆内接四边形
∴α=180°-∠A
∵∠A=90°-β
∴α=180°-(90°-β)=β+90°.
点评:解决本题要熟悉圆中的有关性质,并能灵活的贯穿运用.对于找某两个量之间的数量关系时,先找到与其有直接联系的量之间的数量关系,通过数量转换与所求的量之间发生联系后整理即可求解.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
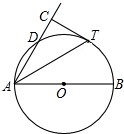 如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.
如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C. 如图,AB是⊙O直径,C、D是⊙O上的两点,若∠BAC=20°,
如图,AB是⊙O直径,C、D是⊙O上的两点,若∠BAC=20°, 如图,AB是⊙O直径,OB=6,弦CD=10,则弦心距OP的长为( )
如图,AB是⊙O直径,OB=6,弦CD=10,则弦心距OP的长为( ) 如图,AB是⊙O直径,弦CD交AB于E,∠AEC=45°,AB=2.设AE=x,CE2+DE2=y.下列图象中,能表示y与x的函数关系是的( )
如图,AB是⊙O直径,弦CD交AB于E,∠AEC=45°,AB=2.设AE=x,CE2+DE2=y.下列图象中,能表示y与x的函数关系是的( )