题目内容
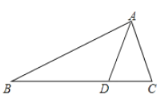
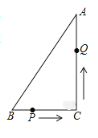
【题目】如图,在△ABC中,BC=7cm,AC=24cm,AB=25cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,请解答下面的问题,并写出探索主要过程:
(1)经过多少时间后,P、Q两点的距离为5![]() cm?
cm?
(2)经过多少时间后,![]() 的面积为15cm2?
的面积为15cm2?
(3)设运动时间为t,用含t的代数式表示△PCQ的面积,并用配方法说明t为何值时△PCQ的面积最大,最大面积是多少?
【答案】(1)经过1秒后,P、Q两点的距离为5![]() cm;(2)经过
cm;(2)经过![]() 或2秒后,
或2秒后,![]() 的面积为15cm2;(3)
的面积为15cm2;(3)![]() =
=![]() ;当
;当![]() 时,
时,![]() 最大,最大面积为
最大,最大面积为![]()
【解析】
(1)连接PQ,根据勾股定理的逆定理可得△ABC为直角三角形,∠C=90°,然后设x秒后,P、Q两点的距离为5![]() cm,根据勾股定理列出方程即可求出结论;
cm,根据勾股定理列出方程即可求出结论;
(2)设y秒后,![]() 的面积为15cm2,根据三角形的面积公式列出方程即可求出结论;
的面积为15cm2,根据三角形的面积公式列出方程即可求出结论;
(3)利用三角形的面积公式即可用含t的代数式表示△PCQ的面积,然后配方,根据平方的非负性即可求出![]() 的取值范围,从而求出其最值.
的取值范围,从而求出其最值.
解:(1)连接PQ,
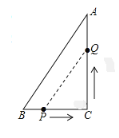
∵在△ABC中,BC=7cm,AC=24cm,AB=25cm,
∴BC2+AC2=625=AB2
∴△ABC为直角三角形,∠C=90°
设x秒后,P、Q两点的距离为5![]() cm
cm
根据题意可得BP=2x,CQ=5x
∴CP=BC-BP=7-2x
根据勾股定理可得CP2+CQ2=PQ2
即(7-2x)2+(5x)2=(5![]() )2
)2
解得:![]() (不符合实际,舍去)
(不符合实际,舍去)
答:经过1秒后,P、Q两点的距离为5![]() cm.
cm.
(2)设y秒后,![]() 的面积为15cm2
的面积为15cm2
根据题意可得BP=2y,CQ=5y
∴CP=BC-BP=7-2y
∴![]()
解得:![]()
答:经过![]() 或2秒后,
或2秒后,![]() 的面积为15cm2.
的面积为15cm2.
(3)根据题意可得BP=2t,CQ=5t
∴CP=BC-BP=7-2t
∴![]() =
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
∵![]()
∴![]()
∴![]() (当且仅当
(当且仅当![]() 取等号),即
取等号),即![]()
![]()
∴当![]() 时,
时,![]() 最大,最大面积为
最大,最大面积为![]() .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案