题目内容
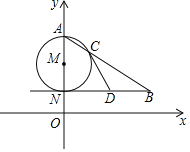
【题目】如图，抛物线y=﹣x2﹣2x+3与x轴交于A、B两点，与y轴交于C点，M点在抛物线的对称轴上，当点M到点B的距离与到点C的距离之和最小时，点M的坐标为_____．
【答案】（﹣1，2）．
【解析】
因为点B关于对称轴的对称点为点A，连接AC，设直线AC与对称轴x=﹣1的交点为M，则此时MB+MC的值最小，再求得点M的坐标即可．
∵抛物线y=﹣x2﹣2x+3与x轴交于A、B两点，令y=0，得：﹣x2﹣2x+3=0，解得：x=－3或x=1，∴点A（﹣3，0），C（0，3）．
设直线AC的解析式为y=kx+b，把A（﹣3，0）、C（0，3）分别代入直线y=kx+b，得：
，解得：
，∴直线AC解析式为y=x+3；
设直线AC与对称轴x=﹣1的交点为M，则此时MB+MC的值最小．
把x=﹣1代入直线y=x+3得：y=2，∴M（﹣1，2）．
即当点M到点B的距离与到点C的距离之和最小时M的坐标为（﹣1，2）．
故答案为：（﹣1，2）．
练习册系列答案
优化作业上海科技文献出版社系列答案
相关题目
