题目内容
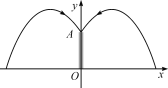
【题目】某市民广场有一个直径16米的圆形喷水池，喷水池的周边有一圈喷水头(喷水头高度忽略不计)，各方向喷出的水柱恰好在喷水池中心的装饰物OA的顶端A处汇合，水柱离中心3米处达最高5米，如图所示建立直角坐标系．王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的他站立时必须在离水池中心O________米以内．
【答案】7
【解析】
根据顶点坐标可设二次函数的顶点式，代入点（8，0），求出a值，求出函数解析式，利用二次函数图象上点的坐标特征，求出当y=1.8时x的值，由此即可得出结论；
设水柱所在抛物线（第一象限部分）的函数表达式为y=a（x－3）2+5（a≠0），
将（8，0）代入y=a（x－3）2+5，得：
25a+5=0，
解得：a=－
，
∴水柱所在抛物线（第一象限部分）的函数表达式为y=－（x－3）2+5（0＜x＜8）．
当y=1.8时，有－（x－3）2+5=1.8，
解得：x1=－1（舍去），x2=7，
∴为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心7米以内．
故答案为：7
练习册系列答案
阅读快车系列答案
相关题目
