题目内容
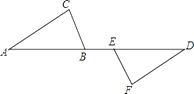
【题目】如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.
求证:
(1)CE=AC+DC;
(2)∠ECD=60°.
【答案】
(1)证明:∵△ABC、△ADE是等边三角形,
∴AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即:∠BAD=∠CAE,
∴△BAD≌△CAE,
∴BD=EC,
∵BD=BC+CD=AC+CD,
∴CE=BD=AC+CD
(2)
证明:由(1)知:△BAD≌△CAE,
∴∠ACE=∠ABD=60°,
∴∠ECD=180°﹣∠ACB﹣∠ACE=60°,
∴∠ECD=60°
【解析】(1)根据△ABC、△ADE都是等边三角形,得到AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,推出∠BAD=∠CAE,得到△BAD≌△CAE,根据全等三角形的性质得到BD=EC,即可推出答案;(2)由(1)知:△BAD≌△CAE,根据平角的意义即可求出∠ECD的度数.
【考点精析】本题主要考查了对顶角和邻补角和等边三角形的性质的相关知识点,需要掌握两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个;等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.

练习册系列答案
相关题目