Question

【题目】如图，已知AE=DB，BC=EF，AC=DF，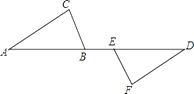
求证：
（1）AC∥DF；
（2）CB∥EF．

Answer 1

【答案】
（1）证明：∵AE=DB，∴AE-BE=DB-BE，
即AB=DE，
在△ABC和△DEF中，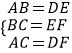
，
∴△ABC≌△DEF（SSS），
∴∠A=∠D，∠ABC=∠DEF，
∴AC∥DF
（2）证明：由（1）得：∠ABC=∠DEF，∴∠CBE=∠FEB，
∴CB∥EF
【解析】（1）由线段的和差和全等三角形的判定方法SSS，得到△ABC≌△DEF，由全等三角形的性质，得到∠A=∠D，再由内错角相等，两直线平行，得到AC∥DF；（2）由（1）得∠ABC=∠DEF，根据等角的补角相等，得到∠CBE=∠FEB，再由内错角相等，两直线平行，得到CB∥EF.