题目内容
【题目】如图，在△ABC中，AB＝AC，点D在AC上，过点D作DF⊥BC于点F，且BD＝BC＝AD，则∠CDF的度数为_____．
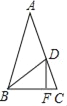
【答案】18°
【解析】
设∠A＝α，可得∠ABD＝α，∠C＝∠BDC＝2α，∠ABC＝2α，再根据△ABC中，∠A+∠ABC+∠C＝180°，即可得到∠C的度数，再根据DF⊥BC，即可得出∠CDF的度数．
解：∵AB＝AC，BD＝BC＝AD，
∴∠ACB＝∠ABC，∠A＝∠ABD，∠C＝∠BDC，
设∠A＝α，则∠ABD＝α，∠C＝∠BDC＝2α，∠ABC＝2α，
∵△ABC中，∠A+∠ABC+∠C＝180°，
∴α+2α+2α＝180°，
∴α＝36°，
∴∠C＝72°，
又∵DF⊥BC，
∴Rt△CDF中，∠CDF＝90°﹣72°＝18°，
故答案为：18°．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某公司有火车车皮和货车可供租用，货主准备租用火车车皮和货车运输一批物资，已知以往用这种火车车皮和货车运货情况如下表：
第一次 | 第二次 | |
火车车皮（节） | 6 | 8 |
货车（辆） | 15 | 10 |
累计运货（吨） | 360 | 440 |
（1）每节火车车皮和每辆货车平均各装物资多少吨？
（2）若货主需要租用该公司的火车车皮7节，货车10辆，刚好运完这批货物，如按每吨付运费60元，则货主应付运费总额为多少元？
（3）若货主共有300吨货，计划租用该公司的火车车皮或货车正好（每节车皮和每辆货车都满载）把这批货运完，该公司共有哪几种运货方案？写出所有的方案．
